На протяжении последних занятий мы с вами учились устанавливать зависимости между величинами, строить информационные модели различными методами, а затем делать прогноз по полученной модели.

Сегодня на уроке мы:
• повторим основные приёмы при построении информационных моделей;
• а также рассмотрим примеры использования табличного процессора для реализации и исследования моделей из различных предметных областей.

Как вы помните компьютерные модели незаменимы в тех случаях, когда реальные эксперименты невозможны или затруднены из-за финансовых или физических препятствий (например, в атомной и ядерной физике, астрофизике).
Процесс разработки моделей и их исследование на компьютере можно разделить на несколько основных этапов:
· Постановка задачи: описание объекта и определение цели моделирования.
· Затем разработка плана создания модели. Здесь необходимо выделить свойства объекта, существенные для данной задачи, и отбросить второстепенные.
· Далее переход к математической модели, а следом создание алгоритма и написание программы.
· И последнее что необходимо сделать – проанализировать модель на соответствие объекту-оригиналу.

При решении задач с помощью электронных таблиц удобно использовать следующую табличную схему модели:

По данной схеме сразу понятно куда следует вводить: Название модели, исходные и начальные данные, а также расчётные формулы.
Рассмотрим первый пример решения экологической задачи.
В результате сброса промышленных стоков возрос уровень загрязнения реки. Необходимо, по данным, приведённым в таблице, определить, каков будет уровень загрязнения реки через сутки, двое и так далее. А также, определить через сколько суток уровень загрязнения станет допустимым, если известно, что за сутки он уменьшится в определённое количество раз.

Здесь C0 нулевое и C допустимое – это начальная и предельно допустимая концентрация вредных веществ; а К – это коэффициент суточного уменьшения концентрации вредных веществ. Буквой N обозначим количество суток, необходимых для уменьшения концентрации вредных веществ в реке.
Приступим к плану создания модели. Здесь объектом исследования является концентрация вредных веществ. Известно, что в зависимости от типа загрязнения, вида реки и других факторов концентрация за сутки уменьшится в определённое количество раз.
Также известны начальная, предельно допустимая концентрация вредных примесей и коэффициент, который показывает, во сколько раз за сутки уменьшится загрязнённость. Чтобы узнать концентрацию вредных примесей на каждые сутки, будем строить таблицу значений концентрации. Для вычислений воспользуемся табличным процессором Excel.

Перейдём к построению математической модели.
Пусть C1, C2, C3 и так далее – концентрация через одни, двое, трое и так далее суток после сброса. Тогда C1=C0\K, C2=C1\K.
Представим задачу в математическом виде. При заданных C0 и ка найти целое значение N, при котором CN будет меньше или равно заданной величине C допустимое.

Приступим к компьютерному построению модели. Для решения задачи в Excel, создадим таблицу с исходными данными.
Теперь заполним расчётную таблицу.
В столбец «Сутки» введём числа от 0 и предположим пока до 300. Если при решении задачи понадобится, то мы увеличим количество суток.
Заполним столбец «Свинец». В ячейку Б10 необходимо ввести начальное значение концентрации вещества, то есть: равно Б4. Далее нам известно, что концентрация каждые следующие сутки уменьшается в Ка раз. Значит, в ячейку Б11 вводим формулу: равно Б10 разделить на Д4, причём ссылка на ячейку Д4 – абсолютная. Теперь скопируем формулу в диапазон ячеек от Б12 до ячейки, в которой значение концентрации достигнет допустимого значения.
Аналогично заполним в расчётной таблице столбцы для мышьяка и фтора.
Следующим этапом разработки и исследования модели является проверка её адекватности.
Мы построили модель в соответствии с условием задачи.
Теперь, сравнивая полученные значения концентраций веществ с допустимой концентрацией, находим номер суток, на которые концентрация вредного вещества станет допустимой.
Мы получили ответ: концентрация свинца в реке достигнет допустимой нормы через 48 суток, мышьяка через 98 суток и фтора через пятьсот тридцать два дня.
То есть для очищения реки от некоторых вредных примесей понадобится полтора года, при условии, что сброс промышленных стоков прекратится.
Рассмотрим следующий пример.
Экономическая задача.
Торговое предприятие имеет сеть, состоящую из 12 магазинов. Информация об их деятельности, представлена в таблице. Руководство предприятия решило выяснить, как зависит размер годового товарооборота от торговой площади магазина.

Решим данную задачу с использованием метода наименьших квадратов.
Пусть у — это годовой товарооборот магазина, измеряется в миллионах рублей; а х — это торговая площадь магазина, измеряется в тысячах метров квадратных.

Для того, чтобы получить формулу мы сначала по данным, полученным математическими статистами построим диаграмму.
Затем, к диаграмме нужно подобрать функцию. Как вы помните, для этого рассматривают стандартные функции.
На основании диаграммы можно сделать вывод о позитивной зависимости годового товарооборота от торговой площади (то есть y будет расти с ростом икс).

Наиболее подходящая форма функциональной связи — линейная.

Напомним, полученную таким образом функцию в статистике называют регрессионной моделью.
То есть регрессионная модель – это функция, описывающая зависимость между количественными характеристиками сложных систем.

Затем, после выбора подходящих функций мы подбирали коэффициенты для них. Причём так, чтобы полученный график функции располагался как можно ближе к экспериментальным точкам. Здесь мы применяли метод наименьших квадратов.
По данному методу искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.

Теперь, получим график регрессионной модели, который называется трендом.

Выделим диапазон ячеек C2 C13, далее на вкладке вставка, в разделе Диаграммы выбираем График, затем график с маркерами.
Нам нужно построить линейную линию тренда. Для этого выделим наш график и нажимаем Конструктор. В разделе Макеты диаграмм нажимаем на значок раскрывающегося списка Добавить элемент диаграммы. Здесь выбираем Линия тренда, затем линейная линия тренда. Снова нажмём на линию тренда и выберем пункт Дополнительные параметры линии тренда.
Здесь нам нужно отметить пункты Показать уравнение на диаграмме и пометить на диаграмму величину достоверности аппроксимации R2.
Теперь на нашем графике мы увидим уравнение линии тренда игрек равно семь целых восемь тысяч триста девять десятитысячных икс плюс семнадцать целых триста девяносто две тысячных. (у=7,8309х +17,392) и величину R2.
В статистике используется величина R2, которая называется коэффициентом детерминированности, он показывает, насколько удачной является полученная регрессионная модель.

Следовательно, можно сделать вывод, при увеличении торговой площади на 1 тысячу квадратных метров, при прочих равных условиях, среднегодовой товарооборот увеличивается на двадцать пять целых две тысячи двести двадцать девять десятитысячных миллиона рублей (25,2229 млн руб).
Рассмотрим следующий пример. При решении которого повторим главные моменты моделей оптимального планирования.
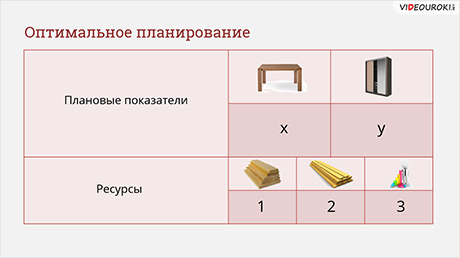
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Нужно определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.

Итак, начнем с составления математической модели задачи. Пусть фабрика изготавливает х столов и у шкафов.
Ресурсами в этом примере можно назвать количество древесины первого и второго вида, а также трудоёмкость, необходимых для изготовления одного изделия.

Прибыль от реализации такого количества шкафов и столов составит:
К прибыли от реализации одного стола нужно прибавить прибыль от реализации одного шкафа и затем эту функцию нужно максимизировать. То есть эф равно 6x + 9у стремится к максимуму.

Теперь составим ограничения задачи.
Для изготовления икс столов потребуется ноль целых две десятых и игрек шкафов – ноль целых одна десятая древесины первого вида, запасы которой составляют 40 кубических метров, поэтому 0,2x + 0,1у должно быть меньше либо равно сорока.
Аналогично составим ограничения для второго и третьего ресурса, а также по смыслу задачи переменные икс и игрек неотрицательны.
Мы получили задачу линейного программирования:
Где F = 6x + 9у стремится к максимуму – целевая функция.

А полученные неравенства являются её ограничениями.
Решим задачу средствами Excel. Заполним ячейки исходными данными (в виде таблицы) и формулами математической модели.
Теперь необходимо вызвать программу оптимизации и сообщить ей, где расположены данные.
На вкладки Данные в группе Анализ выбираем команду Поиск решения. Перед нами открывается соответствующая форма.
Далее необходимо выполнить следующий алгоритм:
Ввести координату ячейки с целевой функцией. В нашем случае это F5. (Заметим, что если перед этим установить курсор на ячейку F5, то ввод произойдёт автоматически).
Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
В поле «Изменяя ячейки переменных» ввести C4:D4, то есть сообщить, какое место отведено под значения переменных-плановых показателей.
В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях следующим образом: щёлкнуть по кнопке «Добавить».
Итак, первое неравенство имеет вид 0,2x + 0,1y меньше либо равно 40. Теперь в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку G10, выбрать из меню знак неравенства меньше либо равно и ввести ссылку на ячейку F10; снова щёлкнуть по кнопке «добавить» и аналогично ввести второе ограничение G11 меньше либо равно F11 и так далее. В конце нажимаем ОК.
Закрываем диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения».
После завершения ввода всех ограничений и параметров нажимаем «Найти решение» и получаем искомое решение задачи.
Решение данной задачи представлено в дробных числах, но так как у нас в задаче нужно найти количество столов и шкафов, а оно не может быть дробным числом, то мы округляем их до целых.
То есть в результате применения инструмента Поиск решения, получен следующий оптимальный план по производству столов и шкафов на мебельной фабрике: нужно изготовить 102 стола и 166 шкафов для получения наибольшей выручки.
Сегодня на уроке мы с вами повторили основные приёмы при построении информационных моделей, а также рассмотрели примеры использования табличного процессора для реализации и исследования моделей из различных предметных областей.
Мы очень надеемся, что полученные знания были для вас полезными и в дальнейшем вы будете активно пользоваться табличными процессорами для решения задач компьютерного информационного моделирования.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 4409
4409

