Однажды два друга, Петя и Алёша, решили поиграть в компьютерную игру «Гонки». Петя сказал, что его автомобиль обгонит Алёшин на 100 км за 4 ч. Но Алёша ответил, что Петя просто хвастается, а на самом деле, его машина обгонит Петину. Давайте поможем мальчикам разобраться в этой ситуации, чтобы они больше не спорили по пустякам. А для этого мы сегодня научимся решать задачи на движение из одной точки в одном направлении.
Итак, разберёмся с игрой наших ребят. Вот какая задача получилась.
Из одного города одновременно в одном направлении выехали 2 автомобиля. Один двигался со скоростью 95 км/ч, а второй – со скоростью 78 км/ч. Какое расстояние будет между автомобилями через 4 ч?
Для того чтобы наглядно представить себе, что в задаче известно, а что надо узнать, конечно, составим краткое условие задачи в виде таблицы с неизменными названиями колонок – скорость, время, расстояние.
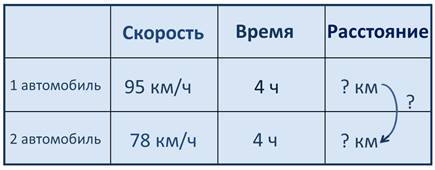
Нам известны скорость первого автомобиля – 95км/ч, и время, которое он находился в пути – 4 ч. Ещё нам известны скорость второго автомобиля – 78 км/ч и то же время – 4 ч. Нам надо найти расстояние между автомобилями.
Посмотрим на рисунок.

Обозначим место выезда автомобилей чертой. Одновременно автомобили выезжают. Через час первый проехал 95 км, а второй – 78 км, прошёл следующий час – и опять 95 км и 78 км, третий час, четвёртый.

Как видим, второй автомобиль уже значительно отстал от первого. Вот это отставание и есть – расстояние между автомобилями через 4 ч. Его мы и должны узнать.
Решить эту задачу можно двумя способами. Рассмотрим первый из них. Вернёмся к нашей таблице. Нам известны скорость и время первого автомобиля. Значит, мы можем узнать расстояние, которое он проехал.
1) Мы 95 · 4 = 380(км) – проехал первый автомобиль.
Теперь узнаем расстояние, которое проехал второй автомобиль.
2) 78 · 4 = 312(км) – проехал второй автомобиль.
Расстояние между автомобилями это тот отрезок пути, насколько первый автомобиль проехал больше, чем второй. Помните правило первого класса? Чтобы узнать, насколько одно число больше или меньше другого мы из большего вычитаем меньшее. Поэтому расстояние между автомобилями мы, конечно, находим вычитанием.
3) 380 – 312 = 68 (км) между автомобилями через 4 ч.
А теперь разберём, как эту же задачу можно решить вторым способом.
Ещё раз посмотрим на рисунок.

Вот выехали два автомобиля. Прошёл час. Первый автомобиль проехал 95 км, а второй – 78 км.

И мы сразу видим, что первый обогнал второго на некоторый отрезок пути, т.к. скорость его больше, чем у второго. Но ведь и за следующий час расстояние между автомобилями увеличится ещё на такой же отрезок. И так за каждый час к тому расстоянию, которое уже есть между автомобилями, добавляются постоянно одинаковые отрезки.

Что же это за отрезки такие? За каждый час первый автомобиль проезжает 95 км, а второй 78 км, значит, первый автомобиль отдалился от второго на некоторое расстояние. Эту разницу мы можем найти действием вычитания.
1) 95 – 78 = 17.
Именно на такое расстояние будет отдаляться первый автомобиль от второго за каждый час. Значит, мы и запишем в пояснении, км/ч. Это – скорость отдаления (или удаления) первого автомобиля от второго. Итак, нам известна скорость отдаления – 17 км/ч и время в пути – 4 ч. А зная скорость и время, мы можем найти расстояние между автомобилями через 4 часа.
2) 17 · 4 = 68 (км)
Ответ: через 4 ч между автомобилями будет 68 км.
Для решения задачи таким способом тоже можно было составить такую же таблицу, лишь немного её изменив. В ней сразу видно, что сначала мы узнаем, на сколько скорость первого автомобиля больше скорости второго, т.е. скорость отдаления. А узнав скорость отдаления и, зная время в пути, мы можем найти расстояние между автомобилями через этот промежуток времени.
Хочу обратить ваше внимание на то, что при решении задач на движение в противоположных направлениях, скорость отдаления находим сложением.

А в задачах на движение из одного пункта в одном направлении скорость отдаления находим вычитание.
̶ Ну все, теперь мы не будем ссориться по пустякам. Мы поняли, что оба были неправы.
̶ Конечно, ведь Петя сказал, что его машина обгонит Алёшину на 100км, а на самом деле обогнала на 68 км. Алёша утверждал, что именно его машина победит в гонках. И он тоже оказался неправ. В споре надо доказывать свою точку зрения не криком, а настоящими доказательствами. В нашей истории это было решение задачи.
̶ А ещё мы теперь научились решать задачи на движение из одной точки в одном направлении.
̶ Очень хорошо. А на что надо обращать внимание при решении задач на движение?
̶ Решая задачи на движение, мы должны обращать внимание на направление движения объектов. Движутся они в одну сторону или в противоположные.
̶ И ещё мы узнали, что при решении задач на движение в одном направлении скорость отдаления находятся вычитанием скоростей движущихся объектов.
Мы это хорошо усвоили. А вы, ребята?

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 13535
13535

