Вспомним ключевые термины прошлого урока.
Системный анализ – это исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.
Модель «чёрного ящика» – это указание входов и выходов системы, а также зависимости между ними.
Модель состава – это своеобразный список элементов системы.

На данном уроке мы с вами узнаем, что такое структурная модель системы, что используется для её отображения, а также вспомним, из чего состоят графы.
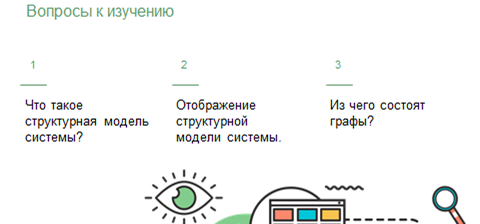
Если обобщить всё пройдённое на прошлом уроке, можно сказать, что модель «чёрного ящика», модель состава и модель структуры полностью описывают систему и образуют ещё одну модель, которая называется структурной моделью системы или структурной схемой. На структурной схеме отражается состав системы и её внутренние связи. Для отображения структурной схемы системы используются графы.
Граф – это совокупность объектов со связями между ними.
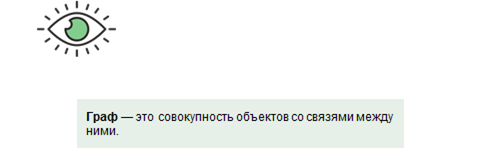
Графически это будет выглядеть следующим образом: вершины (точки) – это элементы системы, а ребра (линии между ними) – это связи (отношения) между элементами системы.
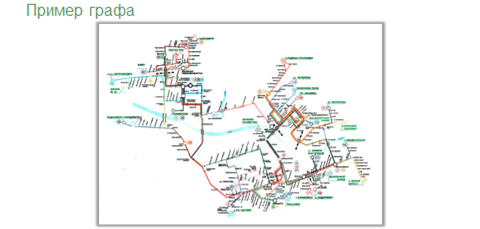
Примером графа является схема движения автобусов в городе, где вершины – это остановки, а рёбра – это пути передвижения автобусов. С помощью такой схемы проще определить на каком автобусе нужно доехать с одной остановки до другой.
Графы бывают ориентированными и неориентированными.

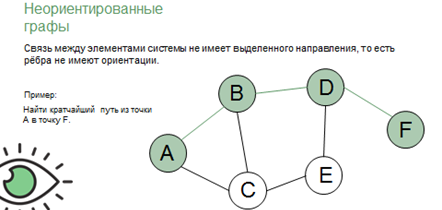
В неориентированных графах связь между элементами системы не имеет выделенного направления, то есть рёбра не имеют ориентации. Примером неориентированного графа будет являться решение задачи на нахождение кратчайшего пути. Граф для решения одной из таких задач, условием которой является нахождение кратчайшего пути из точки A в точку F, будет выглядеть следующим образом.
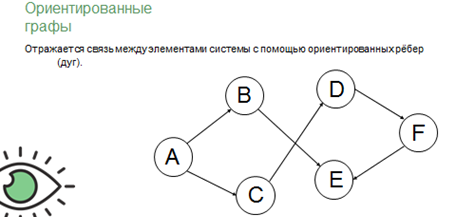
В ориентированных графах наоборот отражается связь между элементами системы с помощью ориентированных рёбер (стрелок). Такие рёбра называются дугами.
Так же с помощью дуг указывается не только наличие связи, но и какой из двух элементов является «началом» связи, а какой «концом». К примеру ориентированного графа можно отнести графическое изображение следующего условия: ученик 11 класса Рома на перемене узнал, что сегодня будет проходить самостоятельная работа по информатике, и решил рассказать об это одноклассникам. Он позвонил Лене, Лена позвонила Маше, Маша рассказала Саше, Саша – Даше, Даша – Кате, Катя – Маше.
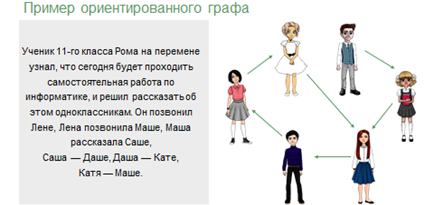
Изобразим каждого учащегося как вершины графа, название которых будут отмечены первыми буквами имён, а звонки или разговоры дугами. Начало дуги будет находиться у вершины учащегося, который рассказывал про самостоятельную, а конец – у вершины того, кому рассказывали. Таким образом, мы получим ориентированный граф.
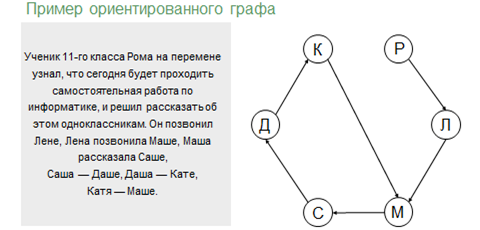
В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.

Ещё графы бывают взвешенными. Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.

Нарисуем взвешенный граф на основе следующего условия: четыре торговца продают друг другу товары. Первый торговец продаёт товар второму по 20 рублей, а четвёртому по 15 рублей. Цена товара у второго торговца для четвёртого составляет 5 рублей, а для третьего – десять. Третий продаёт свой товар первому и четвёртому по 15 рублей, а четвёртый продаёт первому и третьему по 20 рублей. Для обозначения рыночных отношений между торговцами будем использовать дуги, а для указания веса, будем писать его над каждой дугой.
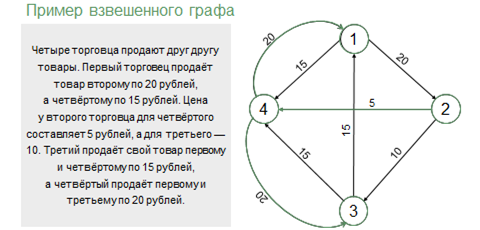
Для начала рисуем все вершины и обозначим их цифрами от одного до четырёх. Затем, по условию задачи первый торговец продаёт свой товар второму и четвёртому. Проведём стрелку от первого ко второму и от первого к четвёртому. Затем над каждой из них запишем соответствующую цену. Таким же образом оформляем весь граф. С помощью данного графа мы можем увидеть, что, например, для четвёртого торговца выгоднее продать товар первому и третьему, а купить у второго. И так далее.
Так же графы бывают связными и несвязными.
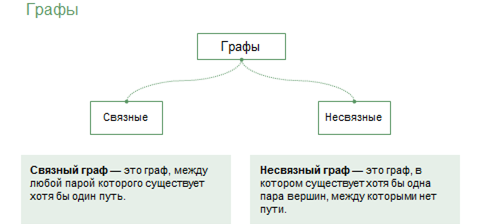
Связный граф – это граф, между любой парой которого существует хотя бы один путь.
Примерами связных графов являются все вышерассмотренные графы.
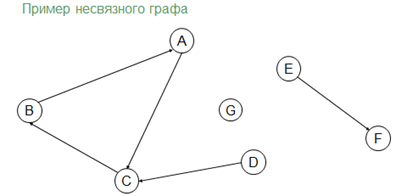
Несвязный граф – это граф, в котором существует хотя бы одна пара вершин, между которыми нет пути. Такие вершины называются несвязными. Например, на показанном графе несвязными вершинами является G и любая другая вершина данного графа.
Следующее понятие, с которым мы должны познакомиться: цепь. Итак, цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза. То есть, при построении пути, по одному и тому же ребру можно пройти только один раз.
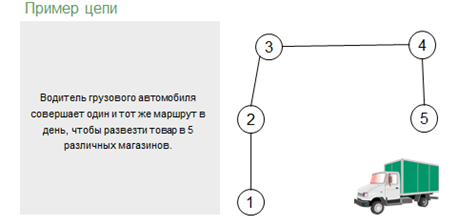
Например, водитель грузового автомобиля совершает один и тот же маршрут в день, чтобы развезти товар в пять различных магазинов. Давайте построим с помощью графа путь водителя. Обозначим вершинами все пять магазинов, и пронумеруем их от одного до пяти. Далее, водитель заехал в первый магазин, выгрузил необходимый товар и поехал во второй магазин. Изобразим ребром путь от первого магазина ко второму. Затем поехал в третий, четвёртый и пятый. Также изобразим данные пути с помощью рёбер. Обратите внимание, что водитель проезжает по каждому ребру только один раз. Данный граф будет являться примером цепи.
Цикл – это цепь, в которой начальная и конечная вершины совпадают.

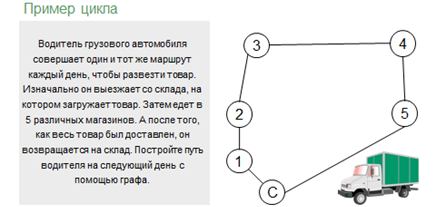
Разберём пример, похожий на предыдущий, но с некоторыми изменениями. Водитель грузового автомобиля совершает один и тот же маршрут каждый день, чтобы развезти товар. Изначально он выезжает со склада, на котором загружает товар. Затем едет в пять различных магазинов. А после того, как весь товар был доставлен, он возвращается на склад. Давайте снова построим путь водителя на следующий день с помощью графа. Обозначим вершинами склад и все пять магазинов, где цифры от одного до пяти будут обозначать магазины, а склад обозначим буквой «С». Изначально водитель заезжает на склад, затем едет в первый магазин, чтобы выгрузить необходимый товар. Обозначим этот путь ребром. Далее он едет из первого магазина во второй. Также изобразим ребром этот путь. Затем водитель едет в третий, четвёртый и пятый магазины. Снова изобразим данные пути с помощью рёбер. Из пятого магазина он едет на склад. Отметим этот путь на нашем графе. Обратите внимание, что водитель проезжает по каждому ребру только один раз и в конце возвращается в первоначальную вершину – на склад. Данный граф будет являться примером цикла.
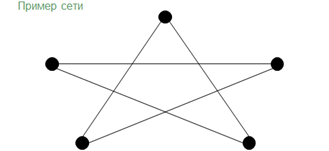
Сеть – это граф с циклом.
В качестве примера сюда можно отнести пятиконечную звезду, но прежде чем проводить ребра, обозначим точкой каждую из вершин. Затем начиная с нижней соединим их.
На практике часто приходится строить системы с иерархической системой. Такой граф называется деревом.
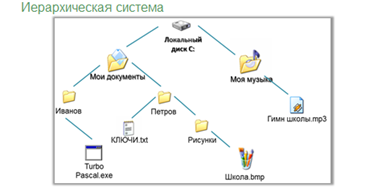
Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь.

Корень дерева – это единственная главная его вершина.

Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков.
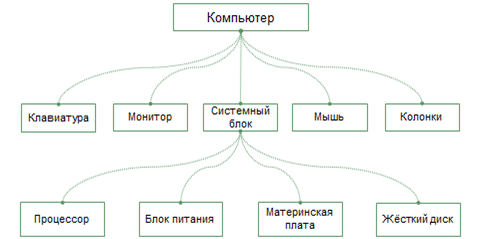
Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим».

Листья – это вершины, которые не имеют потомков.
Разберёмся более подробно на примере.
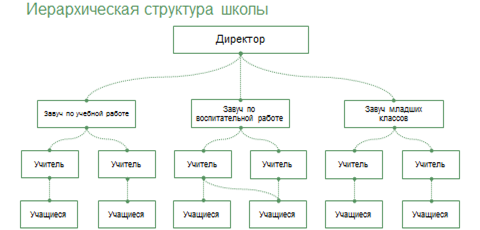
Давайте построим иерархическую структуру школы. Во главе будет находиться директор и соответственно он будет корневой вершиной нашего дерева. Далее на втором уровне будут находиться завуч по учебной работе, завуч по воспитательной работе, завуч младших классов, далее учителя и учащиеся. В данной структуре мы можем видеть, что Потомками являются все, кроме директора, предками – все, кроме учащихся, а листьями – учащиеся, так как в данной структуре у них нет потомков.
Итоги урока:
· Структурная модель системы отражает состав и внутренние связи системы.
· Граф – это графическое отображение структурной модели; состоит из вершин и линий (рёбер и дуг).
· Дерево – это ориентированный граф системы с иерархической структурой; связь – «один ко многим».


 Получите свидетельство
Получите свидетельство Вход
Вход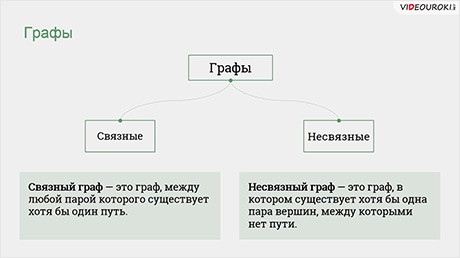



 0
0 19079
19079

