Прямолинейное равноускоренное движение. Ускорение

Известно, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

Ранее рассматривался простейший вид механического движения — равномерное прямолинейное движение. Равномерное движение — это движе­ние, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

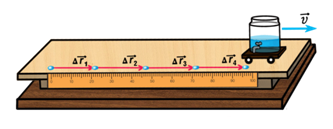
Однако, в повседневной жизни, люди сталкиваются с другим, более сложным видом движения. Трогается или тормозит автомобиль, взлетает или садится самолет. Во всех этих случаях скорость движения постоянно меняется. Такое движение в физике назвали неравномерным.

Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.

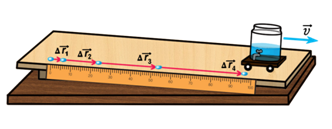
Неравномерное движение бывает двух видов — ускоренным, это когда скорость тела увеличивается с течением времени, и замедленным, когда скорость тела уменьшается с течением времени.

При рассмотрении неравномерного движения пользоваться понятием скорости не целесообразно, так как скорость тела постоянно меняется с течением времени. Поэтому, в некоторых случаях,  пользуются понятием средней скорости.

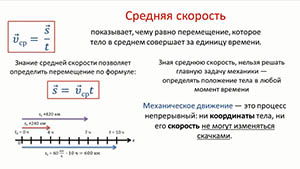
Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу вре­мени.

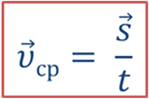
Если, например, троллейбус, двигаясь по прямой, проходит 600 км за 10 ч, то это значит, что в среднем он за каждый час прохо­дит 60 км.

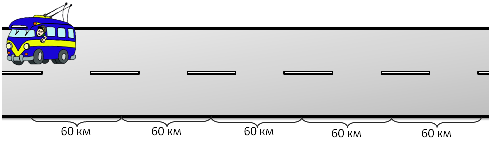
Но ясно, что какую-то часть времени троллейбус вовсе не двигался, а стоял на остановке; трога­ясь с нее, троллейбус увеличивал свою скорость, приближаясь к ней — уменьшал ее. Все это не принимается во внимание и считается, что троллейбускаж­дый час проходитпо 60 км.

Знание средней скорости позволяет определить перемещение по формуле

При этом надо помнить, что эта формула дает верный ре­зультат только для того участка траектории, для которого опре­делена средняя скорость. Если, пользуясь значением средней скорости в 60 км/ч, вычислять перемещение троллейбуса не за 10 часов, а за 4 часа или 7 часов, то мы полу­чим неверный результат.

В данном случае была сделана попытка свести неравномерное движение к рав­номерному движению и для этого была введена средняя скорость движения. Но это нам не помогло: зная среднюю скорость, нельзя решать главную задачу механики — определять положение тела в любой момент времени. Можно ли каким-нибудь другим способом свести не­равномерное движение к равномер­ному?

Этого сделать нельзя, потому что механическое движение — это процесс непре­рывный: ни координаты тела, ни его скорость не могут изме­няться скачками.

Следовательно, в каждой точке траектории движения и в каждый момент времени ско­рость тела имеет определенное значение.

Скорость тела в данный момент времени или в данной точке траектории называют мгно­венной скоростью.

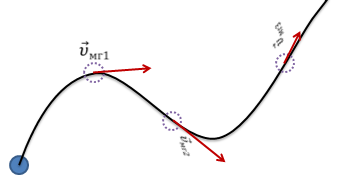
Мгновенная скорость — величина векторная. Она направлена по касательной к траектории в каждой её точке в сторону перемещения.

При неравномерном движении мгновенная скорость тела непрерывно изменяется: от точки к точке, от одного момента времени к другому. Как же вычислить мгновенную скорость тела?

Для вычисления перемещения тела в любой момент времени нужно было знать, как быстро оно изменяется с течением времени. Точно так же для вычисления скорости в любой момент времени нужно знать, как быстро она изменяется, или, говорят, каково изменение скорости в единицу времени.

Для простоты будем рассматривать такое прямолинейное неравномерное движение тела, при котором его ско­рость за любые равные про­межутки времени изменяется одинаково. Такое движение назы­вается равноускоренным.

Если в некоторый начальный момент времени скорость тела равна υ₀, а через некоторый промежуток вре­мени она оказывается равной υ, то за каждую единицу времени скорость изменяется на величину

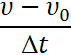
Эта величина  и характеризует быстроту  изменения  скорости. Ее называют   ускоре­нием и обозначают латинской буквой а:

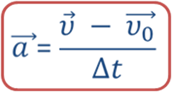
Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение про­изошло.

В системе СИ ускорение измеря­ется в

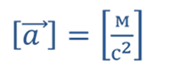
Определим направление вектора ускорения в некоторый момент времени. Для этого необходимо найти вектор изменения скорости тела. Что бы это сделать, необходимо начало вектора υ₀ параллельным переносом совместим с началом вектора υ. Достроим рисунок до треугольника. В результате получаем вектор разности двух векторов. Он направлен в сторону уменьшаемого вектора, в нашем случае, к вектору конечной скорости.

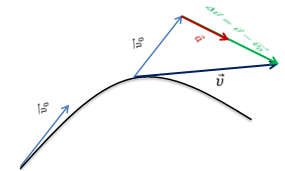
Направление вектора ускорения совпадает с направлением вектора изменения скорости тела.

Рассмотрим связь знаков проекций скорости и ускорения с характером движения тела. Если вектор скорости сонаправлен с вектором ускорения (т.е. вектор скорости направлен в ту же сторону, что и вектор ускорения), то скорость тела увеличивается.

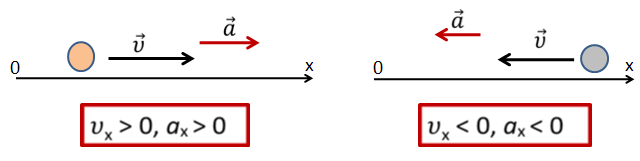
Если вектор скорости направлен в сторону, противоположную вектора ускорения, то скорость тела уменьшается.

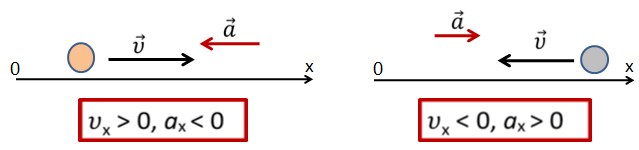
И, наконец, скорость тела постоянна, если вектор ускорения равен нулю или перпендикулярен вектору скорости.

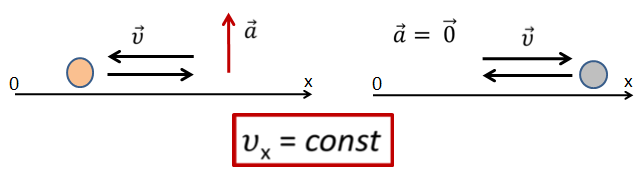
Основные выводы:

·         Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения.

·         В некоторых случаях, когда имеют дело с неравномерным дви­жением, пользуются понятием средней скорости, которая показывает, чему равно перемещение, которое тело в среднем совершает за единицу вре­мени.

·         В каждой точке траектории движения и в каждый момент времени ско­рость тела имеет определенное значение.

·         Скорость тела в данный момент времени или в данной точке траектории называют мгно­венной скоростью.

·         Мгновенная скорость — величина векторная. Она направлена по касательной к траектории в каждой её точке в сторону перемещения.

·         Основной характеристикой неравномерного движения является ускорение. Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение про­изошло.

·         Ускорение измеря­ется в метрах на секунду в квадрате.

·         Если векторы ускорения и скоростисонаправлены, то скорость тела увеличивается.

·         Если векторы ускорения и скорости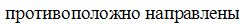, то скорость тела уменьшается.

·         Скорость тела постоянна, если вектор ускорения равен нулюили перпендикулярен вектору скорости.