Видеоучебник / Физика / Видеоуроки. Решение задач по физике. Электродинамика. / Напряженность электрического поля. Принцип суперпозиции полей

Напряженность электрического поля. Принцип суперпозиции полей

Урок 3. Видеоуроки. Решение задач по физике. Электродинамика.

Напряженность является силовой характеристикой электрического поля. Именно с помощью этой величины можно определить силу, с которой тот или иной заряд воздействует на пробный заряд. Если же поле создаётся несколькими зарядами, то применяется принцип суперпозиции полей. Это важнейший принцип, который просто необходимо усвоить для успешного решения задач.

Конспект урока "Напряженность электрического поля. Принцип суперпозиции полей"

«Практика рождается из тесного

соединения физики и математики»

Френсис Бэкон

В данной теме рассмотрим решение задач на напряженность поля.

Задача 1. В некоторой точке поля на заряд 80 нКл действует сила 60 мкН. Найдите напряженность поля в этой точке. Если в эту же точку поместить заряд 200 нКл, то какая сила на него будет действовать?

ДАНО:

СИ

РЕШЕНИЕ

Напряжённость электрического поля в данной точке равна отношению кулоновской силы, действующей на заряд, к величине этого заряда

Тогда

Если поместим другой заряд в эту же точку поля, то напряжённость в ней не изменится

Тогда

Ответ: Е = 667 Н/Кл; F = 150мкН.

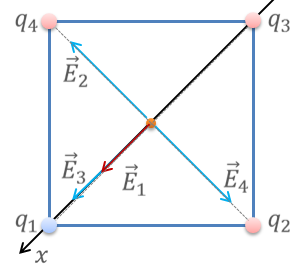
Задача 2. В вершинах квадрата со стороной 40 см находятся заряд q₁ (равный –2 нКл) и заряды q₂, q₃, q₄ (равные 4 нКл). Найдите напряжённость поля в центре квадрата.

ДАНО:

СИ

РЕШЕНИЕ

Поскольку модули положительных зарядов одинаковы, ясно, что напряжённости, создаваемые зарядами q₂ и q₄ компенсируют друг друга в центре квадрата. А вот векторы напряжённости зарядов q₁ и q₃ направлены одинаково, поскольку заряд q₁ отрицательный, а q₃ – положительный. Напряжённость электрического поля, создаваемого несколькими зарядами, определяется, исходя из принципа суперпозиции полей.

Тогда в проекциях на ось Ох

Напряженность поля создаваемая зарядом q определяется по формуле

Расстояние от центра квадрата до заряда определяется по формуле

Тогда напряженность поля создаваемая зарядами q₁ и q₃ равна

Тогда по принципу суперпозиции полей

Ответ: 675 Н/Кл.

Задача 3. . Напряжённость электрического поля на поверхности заряженного шара равна 20 кН/Кл. Найдите модуль силы, действующей на точечный заряд 20 нКл, находящийся на расстоянии 80 см от центра шара. Заряд шара распределён равномерно и равен 3 мкКл.

ДАНО:

СИ

РЕШЕНИЕ

Запишем формулу, по которой рассчитывается напряжённость заряженного шара

В задаче дана напряженность поля на поверхности шара, то есть, при r = R. Это попадает под первый случай. Исходя из этого, можем выразить квадрат радиуса шара

Получаем, что радиус шара больше расстояния между точечным зарядом и центром шара. Значит, для вычисления напряжённости в точке, где находится заряд q, нужно использовать вторую формулу.

Сила, действующая на точечный заряд в данной точке поля, равна

Тогда

Ответ: 276,8 мкН.

Задача 4. Два точечных заряда 30 нКл и –20 нКл находятся на расстоянии 15 см друг от друга. Найдите положение точки на прямой, проходящей через эти заряды, напряженность поля в которой равна нулю.

ДАНО:

СИ

РЕШЕНИЕ

Согласно принципу суперпозиции полей

Напряжённость поля точечного заряда на произвольном расстоянии от него рассчитывается по формуле

Рассмотрим линии напряжённости зарядов на этой прямой. Линии напряжённости направлены от положительного заряда. Также, линии напряжённости направлены к отрицательному заряду. Таким образом, можно убедилиться, что между зарядами q₁ и q₂, векторы напряжённости Е₁ и Е₂ сонаправлены, а, значит, точка, в которой напряжённость равна нулю, не может находится между зарядами. Она находится где-то за зарядом q₂, где векторы напряжённости направлены в противоположные стороны.

Тогда напряженности поля, создаваемые первым и вторым зарядами соответственно равны