– Миша, что случилось? Ты чего такой грустный?

– Я не могу решить задачу по математике. Она очень сложная. И я не знаю к кому мне обратиться за помощью.
– Если хочешь, я могу тебе помочь. Я люблю решать сложные задачи.
– Поможешь, правда?! Тогда слушай задачу.
Два велосипедиста выехали одновременно навстречу друг другу из двух спортивных лагерей и встретились через 3 часа. Первый велосипедист ехал со скоростью 15 км/ч, а второй со скоростью 17 км/ч. Найдите расстояние между спортивными лагерями.
– Так это же задача на встречное движение, обрати внимание «выехали одновременно навстречу друг другу». Ну, давай разбираться.
Давай выполним рисунок к этой задаче.

Итак, обозначим расстояние между двумя спортивными лагерями отрезком. Первый лагерь обозначим буквой А, стрелочкой укажем направление, в котором едет первый велосипедист и укажем его скорость. Второй лагерь обозначим буквой В, так же укажем направление движения и скорость второго велосипедиста. Теперь мы хорошо видим, что движение у нас встречное. Так же мы знаем, что через 3 часа они встретятся. Нам надо узнать, сколько всего км между двумя лагерями.
За час первый велосипедист проехал 15 км, ещё час и ещё 15 км, третий час и снова 15 км. Он доехал до места, где встретился со вторым велосипедистом.

Что же мы можем узнать?
– Мы можем узнать, сколько же км проехал первый велосипедист за 3 часа.
1) 15 · 3 = 45 км.
– Молодец, правильно. Но, второй велосипедист в это время тоже не стоял, а ехал.

Его скорость 17 км/ч, значит за каждый из трёх часов до встречи с первый велосипедистом он проезжал по 17 км. – И мы
2) 17 · 3 = 51 км.
Итак, до встречи первый велосипедист проехал 45 км, а второй 51 км.
– И теперь мы можем узнать, сколько всего км проехали велосипедисты до встречи.
3) 45 + 51 = 96 км. Всего проехали велосипедисты. Значит, расстояние между лагерями 96 км.
Ответ: расстояние между лагерями 96 км.
– Мы посмотрели, как двигались велосипедисты, но ведь они на самом деле двигались не поочерёдно, а одновременно.
– Значит, для решения этой задачи существует и другой способ, да?
– Да, есть и другой способ решения этой задачи. Давай вернёмся к нашему рисунку.

Прошёл час, за это время первый проехал 15 км, а второй в это же время ехал ему навстречу и за час проехал 17 км.

Значит, они приблизились друг к другу на сумму двух этих чисел. Поэтому мы можем узнать, на сколько километров за час велосипедисты стали ближе друг к другу.
1) 15 + 17 = 32 км/ч. Т.к. это сближение произошло за один час, то число 32 является скоростью сближения.
– Повтори, пожалуйста, что такое скорость сближения?
– Это сумма скоростей двух приближающихся друг к другу объектов.
– Так, понятно. Значит, если за первый час два велосипедиста стали ближе друг к другу на 32 км и скорость их движения не меняется, значит, за второй час они приблизятся ещё на 32 км и за третий час – тоже на 32 км.

Вот велосипедисты и встретились. Они до встречи ехали 3 часа, приближаясь за каждый час на 32 км. Поэтому мы
2) 32 · 3 = 96 км.
Ответ: расстояние между лагерями 96 км.
– Давай ещё раз посмотрим внимательно на оба способа решения этой задачи.
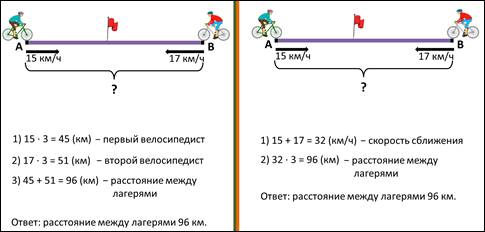
В первом способе мы сначала узнали, сколько км проехал до встречи первый велосипедист, затем узнали, сколько проехал второй велосипедист и после этого нашли всё расстояние между лагерями.
Во втором способе мы сразу узнали, на сколько км за каждый час приближались друг к другу оба велосипедиста, т.е. скорость сближения. А вторым действием узнавали весь пройдённый путь.
– Да, так интересно. Задача одна, а решения два.
– А что ты запомнил, при решении таких задач?
– Если нам надо найти расстояние, для этого мы скорость умножаем на время.

– Правильно, а ещё, т.к. расстояние было пройдено не одним велосипедистом, а двумя вместе, и двигались они на встречу друг другу, то можно использовать такую величину, как скорость сближения. А что такое скорость сближения?
– Это сумма скоростей двух приближающихся друг к другу объектов. В этой задаче такими объектами были велосипедисты.
Ура! Теперь я умею решать задачи на встречное движение. Надеюсь и вы тоже!

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 5900
5900



