Алгоритм письменного приёма деления многозначных чисел

Привет, ребята!

Вы знаете, вчера я услышала разговор двух девочек, которые, как и вы, учатся выполнять письменное деление многозначных чисел на однозначные. И одна из девочек жаловалась другой, что никак не может запомнить последовательность выполнения действий. А вторая девочка посетовала, что иногда запись примеров на деление бывает очень длинной. И поэтому сегодня я решила составить алгоритм письменного деления. А ещё показать, как в некоторых случаях можно немного укоротить запись деления.

И начнём мы с того, что решим вот такой пример: восемь тысяч сто пятьдесят четыре разделим на девять.

Вы помните, с чего всегда необходимо начинать деление? Надо выделить первое неполное делимое. После этого определяем количество цифр в частном и ставим точки на месте частного. Так как восемь меньше девяти, в качестве первого неполного делимого берём две цифры. Это число восемьдесят один. Ставим точку. В делимом есть ещё две цифры, значит, на месте частного ставим ещё две точки.

Восемьдесят один делим на девять, получается девять. Это первая цифра частного. Умножаем девять на девять для того, чтобы узнать, сколько именно мы разделили. Это восемьдесят один. Вычитаем, чтобы узнать остаток. Он равен нулю, который, если деление не окончено, мы не пишем. И, конечно, остаток нуль меньше делителя.

Выделяем второе неполное делимое. Для этого переносим вниз следующую за первым неполным делимым цифру. Второе неполно делимое – пять. Делим его на девять. Так как делимое меньше делителя, то в частном получается нуль. Умножаем нуль на девять. Нуль. Вычитаем. Остаток пять. Сравниваем остаток с делителем. Он меньше делителя.

Выделяем третье неполное делимое. Это пять, что получилось в остатке, и справа от пятёрки дописываем следующую цифру из делимого. Третье неполное делимое – пятьдесят четыре. Делим его на девять, получается шесть. Умножаем. Шестью девять – пятьдесят четыре. Вычитаем. Остаток нуль. Деление закончено.

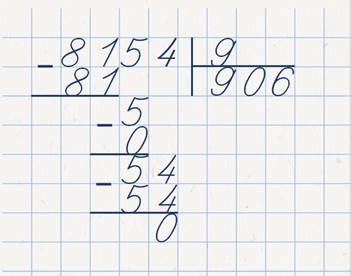
Вы обратили внимание на то, что в приёме письменного деления по нескольку раз повторяются одни и те же фразы?

Сначала выделяется неполное делимое. Затем его делят на делитель. Полученную цифру умножают на делитель. Полученное произведение вычитают из неполного делимого. Остаток сравнивают с делителем. И вновь: выделяем неполное делимое, делим его на делитель, полученную цифру умножаем на делитель, полученное произведение вычитаем из неполного делимого, остаток сравниваем с делителем. И так до тех пор, пока не закончится деление.

Вот у нас и получился алгоритм письменного деления многозначных чисел.

Правда, есть ещё действие, которое выполняется только один раз, после выделения первого неполного делимого. Это – определение количества цифр в значении частного.

Ну а теперь я предлагаю вам посмотреть, как можно запись этого же примера выполнить немного короче.

Начинаю действовать по алгоритму. Выделяю первое неполное делимое, определяю количество цифр в значении частного, делю первое неполное делимое, умножаю полученную цифру, вычитаю полученное произведение. Остаток нуль не пишем, но знаем, что он меньше делителя. Следующее неполное делимое – пять. Так как оно меньше делителя, мы знаем, что, разделив его на девять, получим нуль. Вот теперь ВНИМАНИЕ!!! Мы не будем письменно выполнять деление пяти на девять. Сделаем это устно. Только не забудем записать нуль в частное. А после этого сразу возле пятёрки пишем следующую цифру делимого – четыре. Пятьдесят четыре делим на девять – получается шесть. Умножаем шесть на девять. Вычитаем. Остаток нуль. .

А теперь сравните записи решения одного и того же примера. Как видите, вторая запись немного короче первой, хотя оба примера имеют одинаковый ответ.

Правда, выполняя укороченную запись, очень легко допустить ошибку. Иногда дети перед тем как перенести вниз вторую цифру неполного делимого, забывают поставить в частное нуль.

Чтобы этого не допустить, запомните ребята: если неполное делимое меньше делителя, к нему можно дописать следующую цифру из делимого. Но перед этим в частном обязательно написать нуль!

Вот сейчас попробуйте решить следующий пример, пользуясь укороченной записью.

А теперь проверьте ваше решение. Никто из вас не забыл перед тем, как перенести вниз цифру восемь, написать нуль в частное?

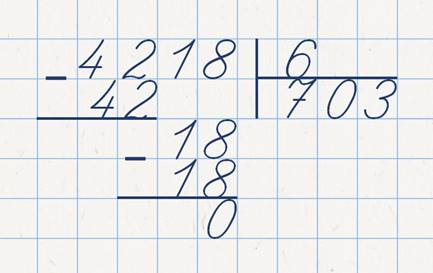
Не забудьте, Если для выделения неполного делимого вниз переносятся две цифры, необходимо в частное написать нуль.

А сейчас я покажу вам ещё один вид примеров, запись которых тоже можно выполнить короче. Это примеры, в которых делимое оканчивается нулями.

Вот, например, разделим двести сорок семь тысяч на пять.

Первое неполное делимое – двадцать четыре. В частном будет пять цифр. Делим двадцать четыре на пять – пишем в частное четыре. Четырежды пять – двадцать. Остаток – четыре. Четыре меньше пяти. Второе неполное делимое – сорок семь. Делим на пять – девять. Умножаем. Сорок пять. Вычитаем. Остаток два. Он меньше делителя. Третье неполное делимое – двадцать. Делим его на пять – четыре. Умножаем. Вычитаем. Остаток нуль. Дальше в делимом стоят два нуля, каждый из которых должен быть неполным делимым. Но когда мы их будем делить, в частном тоже будут нули. Поэтому не будем терять время, а просто перенесём эти два нуля из делимого в частное. Вот так мы сможем сэкономить время и укоротить нашу запись. Но это можно делать только в том случае, если нули стоят в конце делимого. И из делимого в частное переносятся не все нули, а только те, которые должны быть самостоятельными неполными делимыми.

Ну вот, пожалуй, и всё, о чём я сегодня хотела вам рассказать. Но перед тем как попрощаться, я хочу вам напомнить алгоритм приёма письменного деления.

И ещё. Если вы выполняете укороченную запись письменного деления, не забудьте: Переносить из делимого вниз можно только одну цифру. Если же вам нужно перенести и записать рядом вторую цифру, перед этим поставьте в частное нуль.

Ну, а если вы всё-таки забыли это сделать, ещё одна точка в частном, на которой не написали цифру, подскажет вам, что вы допустили ошибку. Так что не забывайте определять количество цифр в частном.

А теперь я прощаюсь с вами. До встречи, друзья!