Пою перед тобой в восторге похвалу
Не камням дорогим, ни злату, но СТЕКЛУ.
М.В. Ломоносов
В рамках данной темы вспомним, что такое линза; рассмотрим общие принципы построения изображений в тонкой линзе, а также выведем формулу для тонкой линзы.
Ранее познакомились с преломлением света, а также вывели закон преломления света. Преломлением света называют изменение направления распространения света, возникающее на границе раздела двух прозрачных сред или в толще среды с непрерывно изменяющимися свойствами.
Закон преломления света звучит следующим образом: луч падающий, луч преломленный и перпендикуляр, восставленный к границе раздела двух сред в точке падения луча, лежат в одной плоскости.

Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред, равная относительному показателю преломления второй походу луча среды относительно первой.

Вообще, слово линза — это слово латинское, которое переводится как чечевица. Чечевица — это растение, плоды которого очень похожи на горох, но горошины не круглые, а имеют вид пузатых лепешек. Поэтому все круглые стекла, имеющие такую форму, и стали называть линзами.

Первое упоминание о линзах можно найти в древнегреческой пьесе Аристофана «Облака» (424 год до нашей эры), где с помощью выпуклого стекла и солнечного света добывали огонь. А возраст самой древней из обнаруженных линз более 3000 лет. Это так называемая линза Нимруда. Она была найдена при раскопках одной из древних столиц Ассирии в Нимруде Остином Генри Лэйардом в 1853 году. Линза имеет форму близкую к овалу, грубо шлифована, одна из сторон выпуклая, а другая плоская. В настоящее время она храниться в британском музее — главном историко-археологическом музее Великобритании.
Линза Нимруда

Итак, в современном понимании, линзы — это прозрачные тела, ограниченные криволинейными поверхностями. Чаще всего используются сферические линзы, у которых ограничивающими поверхностями выступают сферы или сфера и плоскость. В зависимости от взаимного размещения сферических поверхностей или сферы и плоскости, различают выпуклые и вогнутые линзы.
В свою очередь выпуклые линзы делятся на три вида — плоско выпуклые, двояковыпуклые и вогнуто-выпуклая; а вогнутые линзы подразделяются на плосковогнутые, двояковогнутые и выпукло-вогнутые.
Любую выпуклую линзы можно представить в виде совокупностей плоскопараллельной стеклянной пластинки в центре линзы и усеченных призм, расширяющихся к середине линзы, а вогнутую — как совокупностей плоскопараллельной стеклянной пластинки в центре линзы и усеченных призм, расширяющихся к краям.
Известно, что если призма будет сделана из материала, оптически более плотного, чем окружающая среда, то она будет отклонять луч к своему основанию. Поэтому параллельный пучок света после преломления в выпуклой линзе станет сходящимся (такие называются собирающими), а в вогнутой линзе наоборот, параллельный пучок света после преломления станет расходящимся (поэтому такие линзы называются рассеивающими).

Для простоты и удобства, будем рассматривать линзы, толщина которых пренебрежимо мала, по сравнению с радиусами сферических поверхностей. Такие линзы называют тонкими линзами. И в дальнейшем, когда будем говорить о линзе, всегда будем понимать именно тонкую линзу.
Для условного обозначения тонких линз применяют следующий прием: если линза собирающая, то ее обозначают прямой со стрелочками на концах, направленными от центра линзы, а если линза рассеивающая, то стрелочки направлены к центру линзы.
Условное обозначение собирающей линзы

Условное обозначение рассеивающей линзы

Теперь вспомним основные линии и точки линзы, которые изучались в курсе физики 8 класса.
Оптический центр линзы — это точка, пройдя через которую лучи не испытывают преломления.
Любая прямая, проходящая через оптический центр линзы, называется оптической осью.
Оптическую же ось, которая проходит через центры сферических поверхностей, которые ограничивают линзу, называют главной оптической осью.
Точка, в которой пересекаются лучи, падающие на линзу параллельно ее главной оптической оси (или их продолжения), называется главным фокусом линзы. Следует помнить, что у любой линзы существует два главных фокуса — передний и задний, т.к. она преломляет свет, падающий на нее с двух сторон. И оба этих фокуса расположены симметрично относительно оптического центра линзы.
Собирающая линза

Рассеивающая линза

Расстояние от оптического центра линзы до ее главного фокуса, называется фокусным расстоянием.
Фокальная плоскость — это плоскость, перпендикулярная главной оптической оси линзы, проходящая через ее главный фокус.
Рассмотрим основные способы построения изображений в тонких линзах.
При построении изображений предметов в тонкой линзе мы с вами будем в основном пользоваться тремя «удобными лучами» — это лучи, ход которых после прохождения через линзу нам заранее известен.
Собирающая линза

Рассеивающая линза

Во-первых, это лучи, идущие параллельно главной оптической оси, т.к. после преломления в линзе, они проходят через ее главный фокус (или проходят их продолжения).
Из закона обратимости световых лучей следует, что лучи, которые идут к линзе через ее фокус, после преломления будут направлены параллельно главной оптической оси — это второй набор лучей.
И третий набор лучей выбираем исходя из того, что лучи, проходящие через оптический центр линзы, не меняют своего направления.
Приступим непосредственно к построению изображений. Для начала рассмотрим собирающую линзу, фокусы и оптический центр которой заранее известны. Для удобства, расстояние от предмета до линзы будем обозначать маленькой латинской буквой d, а расстояние от линзы до изображения — f.
Построим изображение плоского предмета AB, находящегося на различных расстояниях от линзы.
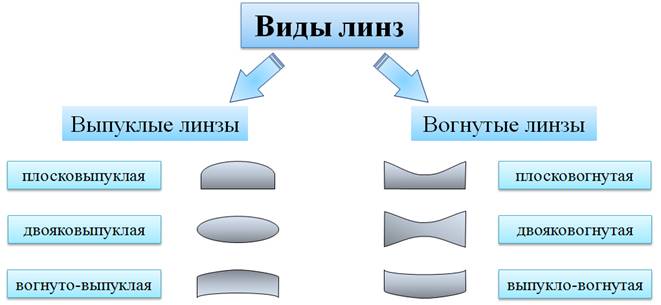
Для начала рассмотрим случай, когда предмет находится за двойным фокусом линзы.
Чтобы построить изображение точки B, направим луч BD параллельно главной оптической оси линзы. После преломления, этот луч, как известно, пойдет через главный фокус линзы. Второй луч BC можно направить через фокус, тогда после преломления в линзе он будет идти параллельно главной оптической оси. В точке пересечения этих двух лучей и будет находиться изображение нашей точки B.
Т.к. наш предмет перпендикулярен главной оптической оси, то теперь достаточно опустить перпендикуляр из точки B1, чтобы получить вторую точку нашего изображения — точку A1. Но важно помнить, что так можно делать только тогда, когда предмет перпендикулярен главной оптической оси.
Можно было бы использовать и луч BO, проходящий через оптический центр линзы.
Таким образом, можно сделать главный вывод о том, что для построения изображения точки достаточно использовать два из трех «удобных» лучей, ход которых через линзу нам заранее известен.
Теперь охарактеризуем полученное изображение. Во-первых, оно действительное, так как получилось на пересечении преломленных лучей. Во-вторых, оно перевернутое. В-третьих, как можно видеть из построения, оно уменьшенное.
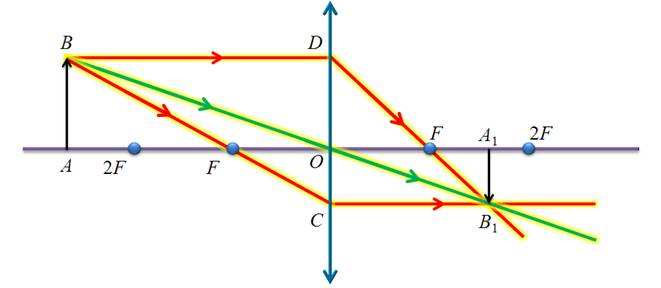
Аналогичным способом, можно построить и охарактеризовать изображение предмета, находящегося на других расстояниях от линзы:
Между первым и вторым фокусом
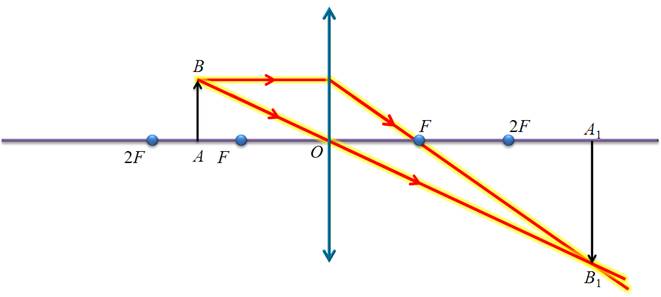
В главном фокусе линзы

Между фокусом и линзой.
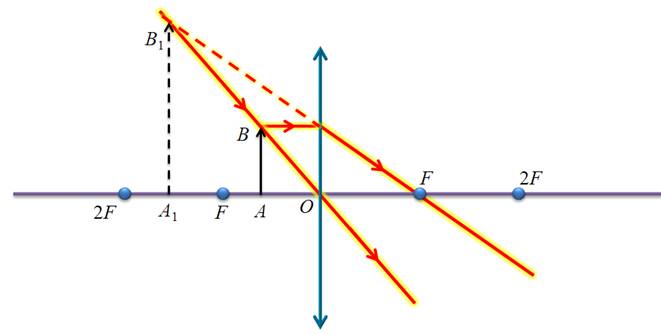
Обратите внимание, что когда предмет располагается между фокусом и линзой, то преломленные лучи расходятся, а пересекаться будут только их продолжения. Поэтому, в этом случае, изображение предмета будет мнимым, увеличенным, прямыми находится со стороны изображаемого предмета.
При построении изображения действительного предмета в рассеивающей линзе поступают точно также как и в случае с собирающей. Единственное отличие состоит в том, что у рассеивающей линзы фокус мнимый. Поэтому изображение, даваемое рассеивающей линзой, всегда мнимое, уменьшенное, прямое и находится между линзой и ее фокусом со стороны изображаемого предмета.

А что делать, если основание предмета находится на главной оптической оси, но сам предмет не перпендикуляре ней? Как строиться изображение в этом случае?
Основная трудность заключается в построении изображения точки, являющейся основанием предмета. А дело в том, что все три «удобных» луча будут сливаться в один, который совпадает с главной оптической осью линзы.
Для удобства уберем наш предмет, оставив только точку, изображение которой нам надо построить.
Чтобы найти, где образуется изображение нашей точки, проведем два луча: первый луч АО, вдоль главной оптической оси (он проходит через оптический центр линзы, не испытывая преломления), а второй луч, например AK, падающий на линзу в произвольной точке K. Здесь главное помнить, что такой луч, после преломления в линзе, не пойдет через ее главный фокус. Для того чтобы найти дальнейший ход этого луча нам необходимо совершить несколько операций.

Во-первых, проведем побочную оптическую ось, параллельную нашему лучу AK.
Затем начертим заднюю фокальную плоскость в случае собирающей линзы или переднюю — в случае рассеивающей линзы.
Как можно заметить, наша побочная оптическая ось пересеклась с фокальной плоскостью в точке, которую называют побочным фокусом линзы F’. Через этот побочный фокус и пойдут все параллельные побочной оптической оси лучи после преломления в собирающей линзе, или их продолжения в рассеивающей, а следовательно, и наш луч AK. Преломленный луч (или его продолжение) пересечет оптическую ось в точке A1,которая и является изображением точки А.
Выведем формулу, которая свяжет три величины — расстояние от предмета до линзы, расстояние от линзы до изображения и фокус линзы. Рассмотрим собирающую линзу, предмет AB и его изображение в этой линзе A1B1.

Из подобия треугольников

Аналогично, из подобия треугольников

Из построений видно, что

Исходя из этого, можно записать, что

Заменив стороны треугольников через введенные ранее величины, и разделив полученное уравнение на расстояние от линзы до изображения, получим формулу тонкой линзы для рассмотренного случая.

В общем же виде, формула тонкой линзы записывается следующим образом:

Величину, равную обратному фокусному расстоянию линзы, выраженному в метрах, называют оптической силой линзы. Она обозначается большой латинской буквой D и измеряется в диоптриях (сокращенно дптр).

Впервые, полученную нами формулу тонкой линзы, вывел Иоганн Кеплер в 1604 году. Он изучал преломления света при малых углах падения в линзах различной конфигурации.
Для практического использования формулы тонкой линзы, нам следует запомнить правило знаков:
для собирающей линзы, действительных источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают положительными;
для рассеивающей линзы, мнимых источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают отрицательными.
Стоит отметить сразу, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей, продолжения которых пересекаются водной точке.
Как можно заметить, чаще всего, изображение, получаемое с помощью тонкой линзы, отличается своими размерами от предмета. Так вот, это различие между размерами предмета и размерами его изображения принято характеризовать линейным (или поперечным) увеличением линзы.
Линейное увеличение линзы — это отношение линейного размера изображения к линейному размеру предмета. Обозначается оно большой греческой буквой G.

Если вернуться к рисунку для вывода формулы тонкой линзы, то можно заметить, что

Тогда можно записать, что линейное увеличение линзы равно отношению расстояния от линзы до изображения к расстоянию от предмета до линзы.

Основные выводы:
– Линзой называется прозрачное тело, ограниченное криволинейными поверхностями.
– Линзы делятся на собирающие и рассеивающие.
– Оптическая сила линзы — величина, обратная ее фокусному расстоянию.
– «удобные» лучи:
луч, проходящий через оптический центр;
луч, падающий на линзу параллельно главной оптической оси;
луч, проходящий через фокус.
– вывели формулу тонкой линзы


 Получите свидетельство
Получите свидетельство Вход
Вход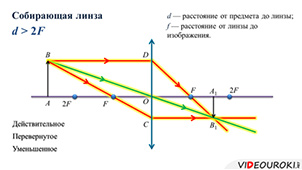



 0
0 26952
26952

