Напомним, что функция 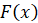 называется первообразной для функции
называется первообразной для функции 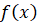 на некотором промежутке, если для всех
на некотором промежутке, если для всех 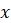 из этого промежутка
из этого промежутка 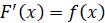 .
.
Операцию нахождения производной данной функции называют дифференцированием. Обратную ей операцию – нахождение первообразной – называют интегрированием.
Вспомним основное свойство первообразных. Каждая
первообразная для функции 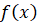 на некотором промежутке может быть
записана в виде
на некотором промежутке может быть
записана в виде 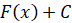 , где
, где 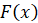 – одна из этих первообразных для функции
– одна из этих первообразных для функции 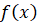 на том же промежутке, а
на том же промежутке, а 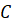 – произвольная постоянная.
– произвольная постоянная.
На следующем слайде приведена таблица первообразных.

Отметим, что множество всех первообразных функции 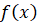 называют неопределённым интегралом этой функции и
обозначают так:
называют неопределённым интегралом этой функции и
обозначают так:
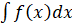 .
.
То есть, если 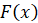 – первообразная для функции
– первообразная для функции 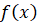 , а
, а 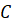 – произвольная постоянная, то
– произвольная постоянная, то  .
.
Вспомним правила нахождения первообразных.
Если функции 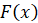 и
и  – первообразные соответственно для функций
– первообразные соответственно для функций 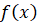 и
и  на некотором промежутке, то функция
на некотором промежутке, то функция  является первообразной для функции
является первообразной для функции  .
.
Если функция 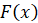 – первообразная для функции
– первообразная для функции 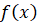 , а
, а  – постоянная, то функция
– постоянная, то функция  является первообразной для функции
является первообразной для функции  .
.
Если функция 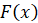 – первообразная для функции
– первообразная для функции 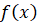 , а
, а  и
и  – постоянные, причём
– постоянные, причём  , то функция
, то функция  является первообразной для функции
является первообразной для функции  .
.
Теперь вспомним, как вычислить площадь фигуры, ограниченной
графиком непрерывной и неотрицательной на отрезке  функции
функции  , осью
, осью  и прямыми
и прямыми  ,
,  . Такую фигуру называют криволинейной трапецией.
. Такую фигуру называют криволинейной трапецией.
Итак, площадь криволинейной трапеции можно вычислить по формуле
 ,
,
где 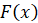 – любая первообразная функции
– любая первообразная функции 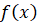 .
.

Разность  называют интегралом функции
называют интегралом функции 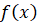 на отрезке
на отрезке  и обозначают
и обозначают  .
.
То есть  . Эту формулу называют формулой Ньютона-Лейбница.
. Эту формулу называют формулой Ньютона-Лейбница.
На практике формулу записывают следующим образом:  .
.
Запись вида  называют определённым интегралом. Числа
называют определённым интегралом. Числа
 и
и  называют соответственно нижним и верхним
пределами интегрирования, функцию
называют соответственно нижним и верхним
пределами интегрирования, функцию 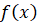 – подынтегральной функцией, переменную
– подынтегральной функцией, переменную 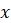 – переменной интегрирования.
– переменной интегрирования.
Напомним два свойства определённого интеграла.
1. 
2. 
Геометрический смысл определённого интеграла заключается в том, что площадь криволинейной трапеции вычисляется
по формуле  .
.
Физический смысл определённого интеграла. При прямолинейном движении перемещение  за промежуток времени от
за промежуток времени от  до
до  вычисляется по формуле
вычисляется по формуле  , где
, где  – скорость движения.
– скорость движения.
Ещё одно физическое истолкование определённого интеграла. Масса  прямолинейного неоднородного стержня с плотностью
прямолинейного неоднородного стержня с плотностью  вычисляется по формуле
вычисляется по формуле  , где
, где  – координата начала стержня,
– координата начала стержня,  – координата конца стержня.
– координата конца стержня.
Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите все первообразные функций:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Решение.



Задание второе. Для функции  найдите первообразную, график которой проходит через точку
найдите первообразную, график которой проходит через точку  .
.
Решение.

Задание третье. Вычислите интегралы:
а)  . б)
. б)  в)
в) 
Решение.


Задание четвёртое. Найдите
площадь фигуры, ограниченной осью  и параболой
и параболой  .
.
Решение.

Задание пятое. Найдите площадь фигуры,
ограниченной осью  , прямыми
, прямыми  ,
,  и графиком функции
и графиком функции  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход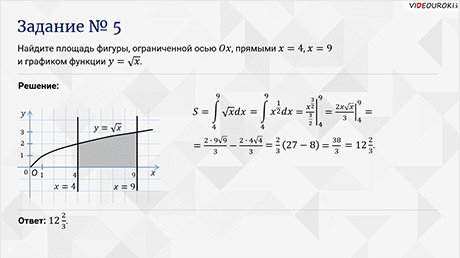




 4318
4318

