Основное уравнение молекулярно-кинетической теории

Самым простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ и начинают с газов. Интересно, что впервые термин «газ» (а «газ» в переводе с греческого означает ‘хаос’) был введён лишь в начале XVII века нидерландским химиком Яном Баптистом ван Гельмонтом.

На прошлом уроке мы с вами говорили о том, что молекулы газа находятся на значительном расстоянии друг от друга и способны к неограниченному расширению. Даже при редких (в масштабах молекул) столкновениях сил притяжения не хватает, чтобы удержать молекулы друг возле друга. Сталкиваясь, они разлетаются в разные стороны, подобно бильярдным шарам. Всё это приводит к тому, что средняя кинетическая энергия теплового движения молекул газа намного больше средней потенциальной энергии их взаимодействия. Поэтому часто значением последней мы пренебрегаем. Это даёт нам право воспользоваться моделью идеального газа.

Итак, идеальный газ — это модель газа, удовлетворяющая следующим условиям: молекулы газа можно считать материальными точками, которые хаотически движутся; силы взаимодействия между молекулами идеального газа практически отсутствуют (они действуют только при столкновении молекул); при столкновениях молекулы идеального газа ведут себя как абсолютно упругие шарики.

При изучении механики мы с вами вводили понятие «механической системы тел» и говорили о том, что состояние любой механической системы определяется её параметрами — координатами, скоростями и импульсами.

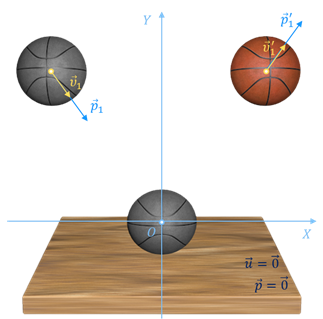
В тепловых процессах основными физическими величинами, характеризующими некоторое количество идеального газа как макроскопическую систему, являются давление, объём и абсолютная температура. Эти физические величины называют макроскопическими параметрами состояния газа.

А к микроскопическим параметрам состояния газа относят индивидуальные характеристики молекул: массу отдельной молекулы, её скорость, импульс и кинетическую энергию теплового движения.

Одна из важнейших задач молекулярно-кинетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами. Найдём эту связь. Для этого предположим, что у нас есть закрытый сосуд в форме куба, в котором находится идеальный одноатомный газ, находящийся в термодинамическом равновесии (так принято называть состояние, в котором все макроскопические параметры газа остаются неизменными во времени по всему объёму). Ещё в седьмом классе мы говорили о том, что газ, находящийся в сосуде, будет оказывать давление на его стенки. С точки зрения молекулярно-кинетической теории это давление вызвано ударом молекул газа о стенки сосуда. Очень слабые силы ударов отдельных молекул складываются для громадного количества молекул в значительную по величине и почти постоянную силу, действующую на тело. Усреднённое по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа.

Итак, пусть молекула идеального газа массой т₀ движется перпендикулярно стенке куба с некоторой постоянной скоростью. В результате абсолютно упругого удара со стенкой сосуда молекула газа передаст участку стенки определённый импульс, а направление скорости молекулы измениться на противоположное. Тогда проекция изменения её импульса будет равна разности проекций импульсов до и после взаимодействия:

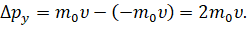
Для определения давления на стенку куба необходимо вычислить совокупное воздействие молекул на неё за некоторый промежуток времени.

Для этого необходимо умножить изменение импульса одной молекулы на полное число молекул, ударяющихся о стенку за данный промежуток времени:

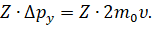
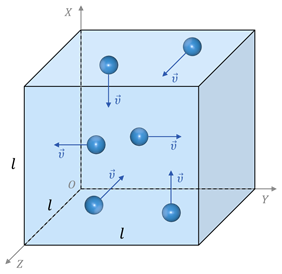
Теперь предположим, что в кубе хаотично движется N молекул. Так как газ у нас находится в термодинамическом равновесии, то из-за беспорядочного движения молекул результат их удара о стенки таков, как если бы треть всех молекул двигалась прямолинейно между правой и левой стенкой, треть — между передней и задней стенкой и треть — между верхней стенкой и нижней. А так как все направления в пространстве равноправны, то число молекул, летящих к выбранной грани куба, составляет шестую часть всех молекул, заключённых в сосуде:

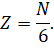
Выберем промежуток времени таким образом, чтобы все молекулы, находящиеся в сосуде, успели хотя бы раз столкнуться с одной из граней куба. При этом время полёта молекулы от одной грани до другой будет определяться отношением длины ребра куба к скорости молекулы:

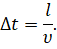
Тогда суммарное изменение импульса молекул за счёт столкновения с выбранной гранью за время ∆t будет определяться выражением, которое вы видите на экране:

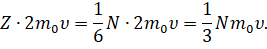
С другой стороны, мы с вами знаем, что изменение импульса молекул может быть определено и на основании второго закона Ньютона, записанного в импульсной форме:

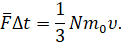
Здесь 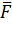 — это средняя сила реакции, действующая со стороны грани сосуда на молекулы. Она, по третьему закону Ньютона, равна по модулю силе, с которой поток молекул воздействовал на стенку. Теперь вспомним, что по определению давление газа — это средняя сила воздействия его молекул, отнесённая к единице площади:

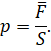
Значение средней силы мы выразим из второго закона Ньютона:

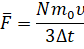
А время полёта молекулы от одной грани до другой мы с вами нашли ранее. Давайте подставим выражения для промежутка времени и средней силы в формулу давления:

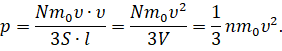
Теперь вспомним, что произведение площади грани на её ребро — это есть объём куба (в нашем случае это объём сосуда, в котором находится газ). А число молекул газа в единице объёма — это концентрация молекул.

Таким образом, мы с вами нашли давление газа для идеального случая. В реальных же условиях молекулы движутся не только хаотически, но и имеют различные скорости, что не было нами учтено. Однако, как показали расчёты, среднее значение модуля этих скоростей имеет вполне определённое значение:

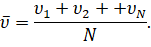
То же самое будет относиться и к среднему значению квадрата скорости молекул:

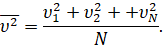
Перепишем формулу для давления газа с учётом этой поправки:

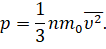
Полученное нами уравнение носит название основного уравнения молекулярно-кинетической теории газов. Оно связывает макроскопическую величину — давление, которое может быть непосредственно измерено с микроскопическими параметрами молекул: массой и скоростью их хаотичного движения.

А теперь давайте проделаем такую операцию: умножим и разделим на 2 правую часть основного уравнения МКТ

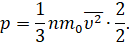
И поменяем местами сомножители:

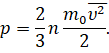
 Множитель 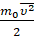 — это средняя кинетическая энергия поступательного движения молекул.

Тогда можно записать, что давление идеального газа равно двум третям средней кинетической энергии поступательного движения всех молекул, заключённых в единице объёма:

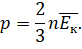
Это уравнение тоже можно назвать основным уравнением молекулярно-кинетической теории. Но связывает оно уже другие параметры: макропараметр давление со средней кинетической энергией их поступательного движения, являющейся с микроскопической характеристикой.

Эта формула впервые была получена немецким физиком Рудольфом Клаузиусом, и поэтому её часто называют уравнением Клаузиуса.

Для примера решим с вами задачу. Кислород находится под давлением 95 кПа и имеет плотность 2,1 кг/м³. Определите среднюю кинетическую энергию поступательного движения его молекул.