Колебательное движение. Свободные колебания. Колебательные системы. Маятник

Рожденный пустыней,

Колеблется звук,

Колеблется синий

На нитке паук.

Колеблется воздух,

Прозрачен и чист,

В сияющих звездах

Колеблется лист.

Николай АлексеевичЗаболоцкий

В данной теме рассмотрим еще один вид неравномерного движения — колебательное движение.

Колебательные движения широко распространены в окружающей нас жизни. Примерами колебаний могут служить: движение иглы швейной машины, качелей, маятника часов, вагона на рессорах, работа сердечной мышцы, колебания дерева на ветру, крыльев птиц, насекомых и многих других тел.

На рисунке изображены тела, которые могут совершать колебательные движения, если их вывести из положения равновесия.

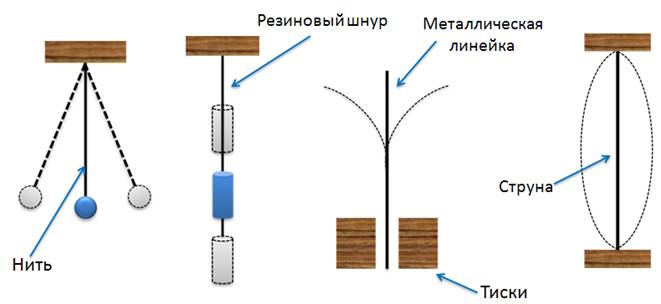
В движении этих тел можно найти много различий. Например, шарик на нити движется криволинейно, а цилиндр на пружине — прямолинейно; верхний конец линейки колеблется с большим размахом, чем средняя точка струны.

Но при всем разнообразии этих движений у них есть важная общая черта: через определенный промежуток времени движение любого тела повторяется.

Движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях, называют механическим колебательным движением.

Действительно, если, например, стрелку метронома отвести от положения равновесия и отпустить, то она, пройдя через положение равновесия, отклонится в противоположную сторону, остановится, а затем вернется к месту начала движения. За этим колебанием последует второе, третье и т. д., похожие на первое.

Если состояния движения тела повторяются через определенные промежутки времени, то колебания называются периодическими.

Таким образом, основным признаком, по которому можно отличить колебательное движение от других видов движения, является периодичность.

Остановимся более подробно на колебаниях.

Рассмотрим шарик прикрепленный к пружине (другой конец которой прикреплен к вертикальной стойке). Шарик может свободно скользить, т. е. силы трения настолько малы, что не оказывают существенного влияния на его движение. Когда шарик находится в точке О, пружина не деформирована, поэтому никакие силы в горизонтальном направлении на него не действуют. Точка О— положение равновесия шарика.

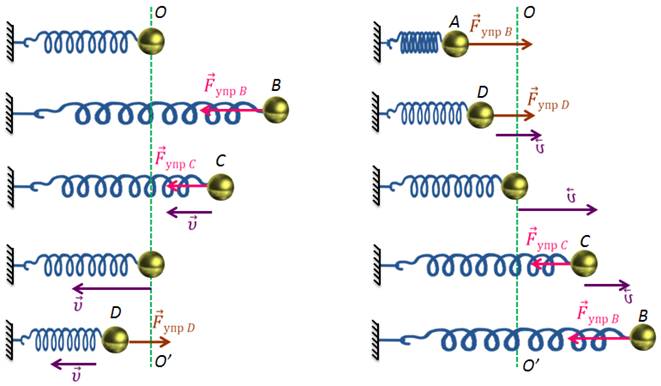
Переместим шарик в точку В. Пружина при этом растянется, и в ней возникнет сила упругости. По закону Гука эта сила пропорциональна смещению (т.е. отклонению шарика от положения равновесия) и направлена противоположно ему. Значит, при смещении шарика вправо действующая на него сила направлена влево, к положению равновесия.

Если отпустить шарик, то под действием силы упругости он начнет ускоренно перемещаться влево, к точке О. Направление силы упругости и вызванного ею ускорения будет совпадать с направлением скорости шарика, поэтому по мере, приближения шарика к точке О его скорость будет все время возрастать. При этом сила упругости с уменьшением деформации пружины будет уменьшаться.

Известно, что любое тело обладает свойством сохранять свою скорость, если на него не действуют силы или если равнодействующая сил равна нулю. Поэтому, дойдя до положения равновесия, где сила упругости станет равна нулю, шарик не остановится, а будет продолжать двигаться влево.

При его движении от точки О к точке А пружина будет сжиматься. В ней снова возникнет сила упругости, которая и в этом случае будет направлена к положению равновесия.

Поскольку сила упругости направлена против скорости движения шарика, то она тормозит его движение. В результате в точке А шарик остановится. Сила упругости, направленная к точке О, будет продолжать действовать, поэтому шарик вновь придет в движение и на участке АО его скорость будет возрастать.

Движение шарика от точки О к точке В снова приведет к растяжению пружины, вследствие чего опять возникнет сила упругости, направленная к положению равновесия и замедляющая движение шарика до полной его остановки. Таким образом, шарик совершит одно полное колебание. При этом в каждой точке его траектории (кроме точки О) на него будет действовать сила упругости пружины, направленная к положению равновесия.

Под действием силы, возвращающей тело в положение равновесия, тело может совершать колебания как бы само по себе. Первоначально эта сила возникла благодаря тому, что была совершена работа по растяжению пружины, сообщив ей некоторый запас энергии. За счет этой энергии и происходили колебания.

Если колебания происходят в системе благодаря начальному запасу энергии, или, говорят, только под действием внутренних сил, то такие колебания называют свободными.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая получила название колебательной системы.

Колебательная система — это физическая система, в которой при отклонении от положения равновесия возникают и существуют колебания

В рассмотренном примере в колебательную систему входят шарик, пружина и стойка, к которой прикреплена пружина.

Рассмотрим другую колебательную систему, состоящую из шарика, нити, штатива и Земли (Земля на рисунке не показана).

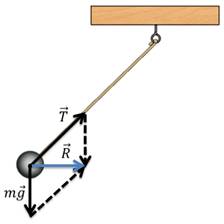
В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити. Их равнодействующая направлена к положению равновесия.

Что же необходимо для того, чтобы свободные колебания возникли? Сформулируем условия возникновения колебаний в системе.

Для этого рассмотрим следующие примеры. Вот три положения тела: в чашке, на перевернутой чашке и на горизонтальном столе.

Что произойдет, если отпустить тело или толкнуть его, добавив при этом избыток энергии. Тело в чашке начнет совершать колебательные движения туда и обратно. То что находится на чашке — скатится, и никакого колебательного движения не будет. Тело же, находящееся на горизонтальной поверхности покатится в сторону и со временем остановится.

Напомним, что существуют три типа равновесия тела: устойчивое, неустойчивое и безразличное.

1) Для того, чтобы в системе возникли свободные колебания, обязательно необходимо наличие положения устойчивого равновесия системы — это такое положение, где равнодействующая сила равна нулю.

2) Необходимо наличие у тела избыточной механической энергии по сравнению с ее энергией в положении устойчивого равновесия. Так, например, для того чтобы тело в чашке начало совершать колебательное движение, его необходимо вывести из положения равновесия, т.е. сообщить ему избыток потенциальной энергии.

3) Действие на тело возвращающей силы, т.е. силы, направленной всегда к положению равновесия. В нашей системе — это равнодействующая силы тяжести и силы реакции опоры.

4) В идеальных колебательных системах должны отсутствовать силы трения. Т.е. чтобы колебание возникло и продолжалось, избыточная энергия, полученная телом при смещении из положения устойчивого равновесия, не должна быть полностью расходована на преодоление сопротивления при возвращении в это положение.

Вообще, колебательные системы — это довольно широкое понятие, применимое к разнообразным явлениям. Рассмотренные колебательные системы называются маятниками. Существует несколько типов маятников: нитяные, пружинные и т.д.

В общем случае под словом «маятник» понимают твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

Основные выводы:

– Механическое колебательное движение —  движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.

– Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.

– Колебательная система — физическая система, в которой при отклонении от положения равновесия возникают и существуют колебания.

– Маятник — твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.