Вычисление объемов тел с помощью интеграла

Прежде чем мы перейдём к нашей теме, давайте ненадолго вернёмся в алгебру и вспомним формулу Ньютона-Лейбница, которая позволяет нам вычислить определённый интеграл, повторим основные свойства интеграла.

Если функция  непрерывна на отрезке , то справедлива формула:

 – первообразная для .

 − геометрический смысл определённого интеграла.

Изучая алгебру, мы говорили, что с помощью определённого интеграла можно вычислять площадь плоских фигур.

Сегодня на уроке мы попробуем применить определённый интеграл к вычислению объёмов тел.

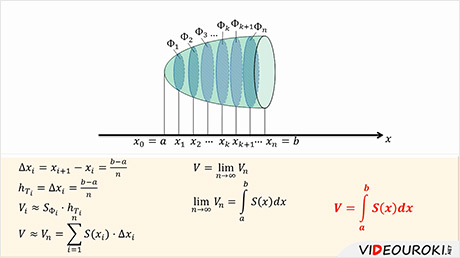
Заключим тело , объём которого нужно найти между двумя параллельными плоскостями  и .

Введём систему координат так, чтобы ось , абсциссы точек пересечения оси  с плоскостями  и  обозначим буквами  и . Пусть .

Пересечём наше тело произвольной плоскостью, перпендикулярной к оси . Фигура  – полученная в сечении тела плоскостью является либо кругом либо многоугольником для любого  из отрезка . В граничных точках сечение может вырождаться в точку, как, например, в нашем случае при .

Обозначим площадь фигуры  за . Предположим, что  – это непрерывная функция на числовом отрезке .

Разобьём числовой отрезок  на  равных отрезков.

Длина каждого отрезка равна .

Через точки с абсциссами  проведём плоскости, перпендикулярные к оси . Тогда наше тело  разобьётся на  тел , , …, .

Высота каждого из этих тел равна .

Если фигура  – круг, то объём тела  приближённо равен объёму цилиндра, с основанием  и высотой .

Если же в сечении – многоугольник, то объём тела  приближённо равен объёму прямой призмы с основанием  и высотой .

Каждый из этих объёмов равен произведению площади основания на высоту . Тогда объём всего тела равен сумме этих объёмов . Чем больше , тем точнее приближённое значение объёма всего тела и меньше .

Без доказательства примем, что объём тела  равен .

С другой стороны, сумма  является интегральной суммой для непрерывной функции  на числовом отрезке , поэтому можно записать, что предел .

Тогда получим, что объем тела  равен .

Эта формула называется основной формулой для вычисления объёмов тел.

Давайте теперь попробуем найти с помощью определённого интеграла объёмы пространственных тел.

Начнём с прямоугольного параллелепипеда, высота которого равна , а площадь основания – .

Площадь сечения прямоугольного параллелепипеда не изменяется в любой точке отрезка от  до  и равна площади основания. Тогда получим, что объём прямоугольного параллелепипеда равен . Вынесем  за знак интеграла и получим, что объём прямоугольного параллелепипеда равен .

Теперь попробуем с помощью интеграла вычислить объём прямой призмы.

Пусть дана прямая  -угольная призма с площадью основания  и высотой .

Как и в случае прямоугольного параллелепипеда, площадь сечения прямой призмы не изменяется в любой точке отрезка от  до  и равна площади основания. Тогда получим, что объём прямой призмы равен . Вынесем  за знак интеграла и получим, что объём прямой призмы равен .

Теперь рассмотрим цилиндр с высотой  и площадью основания .

Как и в случае прямоугольного параллелепипеда и прямой призмы, площадь сечения цилиндра не изменяется в любой точке отрезка от  до  и равна площади основания. Тогда получим, что объём цилиндра равен . Вынесем  за знак интеграла и получим, что объём цилиндра равен .

Решим несколько задач.

Задача: сечение тела плоскостью, перпендикулярной к оси  и проходящей через точку с абсциссой , является квадратом, сторона которого равна . Найти объем этого тела.

Решение: воспользуемся только что доказанной формулой.

По рисунку видно, что пределами интегрирования будут числа . Поскольку сечение плоскости – квадрат, значит, площадь сечения равна .

Тогда получим, что объём этой фигуры равен .

Задача: найти объём тела, полученного вращением данной кривой вокруг оси .

Решение: очевидно, что границами интегрирования будут числа .

В сечении полученного тела плоскостью, перпендикулярной оси  будет круг, радиус которого равен ординате точки с абсциссой , то есть радиусом этого круга будет .

Площадь такого круга равна . Поскольку  принимает только неотрицательные значения, то можно записать, что площадь сечения равна .

Вычислим объём полученного тела как . Применив формулу Ньютона-Лейбница, получим, что объём данного тела равен .

Задача: найти объём тела, полученного вращением данной кривой вокруг оси .

Решение: давайте внимательно посмотрим на получившееся тело.

Его можно получить из цилиндра, который получится при вращении прямоугольника вокруг своей стороны. Для этого надо из данного цилиндра «вынуть» фигуру, которую мы получили в предыдущей задаче.

Объём такой фигуры будет равен разности объёмов .

Радиусом основания цилиндра будет ордината точки с абсциссой равной 1. То есть радиус основания цилиндра равен . Высота цилиндра тоже равна . Тогда получим, что объём цилиндра равен .

Тогда объём искомой фигуры равен .

Итоги:

Сегодня на уроке мы показали, что объём геометрического тела можно найти с помощью определённого интеграла. Определили объёмы известных нам тел через интегралы. Рассмотрели несколько задач.