Вопросы:
· Правила преобразования числовых типов данных.
· Операции и функции над выражениями числовых типов.
· Целочисленные типы данных.
Рассмотрим правила преобразования числовых типов в среде программирования Pascal ABC. И так к числовым типам данных относятся целочисленные типы: byte и integer, а также вещественный тип real. Мы можем легко преобразовать переменные типа byte в тип integer или даже real. Достаточно просто присвоить переменной типа integer или real значение переменной типа byte. Точно также можно перевести переменные типа integer в real. Переменные вещественного типа real нельзя перевести в целочисленный тип неявно. Это можно сделать только с помощью специальных функций, которые мы рассмотрим позже. Переменные типа integer также можно неявно преобразовать в byte, но это происходит немного сложнее. Если значение исходной переменной соответствует диапазону типа byte, то есть находится в промежутке от 0 до 255, то значение результирующей переменной будет равно значению исходной. Если же значение исходной переменной больше 255 – итоговое значение будет равно остатку от деления исходного на 256. Если же значение исходной переменной будет отрицательным – к нему будет добавляться число 256, до тех пор, пока не будет получено положительное значение, это значение и будет итоговым.
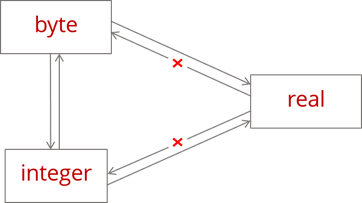
Возможности неявного преобразования данных числовых типов
Рассмотрим операции и функции общие для всех числовых типов. Прежде всего над любыми числами, как над целыми, так и над вещественными можно производить основные арифметические операции: сложение вычитание, умножение и деление. Они записываются соответственно знаками: +, -, * и / и работают над двумя выражениями, которые указываются слева и справа от них. Сложение, вычитание и умножение возвращают результат в зависимости от типа переменных, над которыми производится операция. Если оба аргумента целочисленных типов, то есть byte и integer – то и результат будет целым числом. Если один или оба аргумента принадлежат вещественному типу real, то и результат будет принадлежать типу real. Деление же, независимо от типа аргументов, всегда возвращает результат вещественного типа, real.

Основные арифметические операции
Так же есть ещё две, хорошо знакомые нам, арифметические функции: возведение в квадрат и извлечение квадратного корня из числа. Первая функция записывается английскими буквами sqr, сокращённо от слова square, что в переводе на русский язык означает квадрат. После неё в круглых скобках указывается аргумент. Результат выполнения этой функции будет того же типа, что и аргумент. По тем же правилам записывается функция извлечения квадратного корня из числа она обозначается служебным словом sqrt. Результат выполнения этой функции всегда будет вещественного типа.
Ещё одна функция общая для числовых типов – модуль числа. Как мы помним, модулем числа называется расстояние от начала отсчёта до точки, соответствующей этому числу на числовой оси. То есть если аргумент положительный или нулевой – то эта функция вернёт значение равное аргументу, если же аргумент отрицательный – то функция вернёт значение противоположное аргументу по знаку. Функция модуля записывается сочетанием букв abs её значение будет того же типа, что и аргумент.
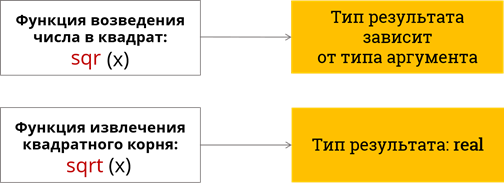
Функции возведения в квадрат и извлечения квадратного корня
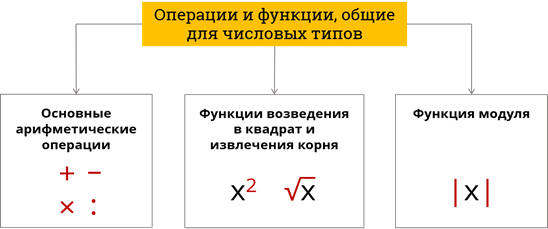
Операции и функции общие для числовых типов
Теперь рассмотрим функции, аргументом которых может быть только вещественное число. Это функция округления, а также функции выделения целой и дробной части. Функция округления записывается служебным словом round, что в переводе на русский язык и означает округление. Значение этой функции имеет целочисленный тип. Функция округления – это единственный способ преобразования вещественных чисел к целому типу. Функции выделения целой и дробной части записываются соответственно int и frac – эти функции возвращают значение вещественного типа.
Отдельно стоит рассмотреть функцию random, которая не имеет аргументов. Эта функция возвращает случайное вещественное число от 0 до 1, при этом 0 входит данный промежуток, а 1 - нет.

Функции вещественного аргумента
Давайте посмотрим, как работают, изученные нами функции. Напишем программу, которая будет генерировать случайное число от 0 до 1, умножать его на 100, после чего выводить на экран: полученное число, его квадрат и квадратный корень, его целую и дробную части и результат его округления до целых.
И так программа начинается со служебного слова program, назовём нашу программу test. Для работы программы нам потребуется одна переменная, назовём её a, по условию он должна выть вещественного типа real. Запишем логические скобки программы. И начнём записывать операторы. В начале нам нужно сгенерировать случайное число от 0 до 1. И присвоить его переменной a. Запишем оператор a:=random. Теперь присвоим переменной a значение a * 100. Далее нам нужно вывести полученное число и всё, что перечислено в условии задачи на экран. Как мы помним это можно сделать с помощью оператора writeln. Далее будет следовать 6 операторов вывода writeln. Cкопируем первый оператор 6 раз.
В первом операторе вывода выведем сначала поясняющее сообщение в виде строкового значения ‘Само число – ‘. После поясняющего сообщение выведем значение переменной a. Второй оператор будет содержать поясняющее сообщение ‘Квадрат – ‘, а также функцию sqrt (a). Следующий оператор будет содержать всё тоже самое для квадратного корня. Функция квадратного корня записывается sqrt. Следующий оператор будет содержать тоже самое для функции выделения целой части числа – int. Следующий – для функции выделения дробной части – frac. И последний для функции округления до целых – round.
program test;
var
a: real;
begin
a:=random;
a:=a*100;
writeln ('Число - ', a);
writeln ('Квадрат - ', sqr (a));
writeln ('Корень - ', sqrt (a));
writeln ('Целая часть - ', int (a));
writeln ('Дробная часть - ', frac (a));
writeln ('Округление - ', round (a));
end.
Исходный код программы
Запустим нашу программу на выполнение и посмотрим на данные которые вывела программа. Обратим внимание на отличие в работе функций int и round. Первая функция просто отбрасывает дробную часть числа, а функция round округляет число до целых по всем правилам математики.

Результат работы программы
Теперь рассмотрим операции и функции, уникальные для целочисленных типов. Помимо функций, и операций общих для всех числовых типов для целочисленных переменных есть две уникальные операции. Это операция безостаточного деления – div. И операция выделения остатка от деления – mod. Результаты этих операций также имеют целочисленные типы. Также для целочисленных типов есть своя функция генерации случайного числа она, так же, как и для вещественных чисел, записывается словом random, после него в скобках указывается целочисленный аргумент. Данная функция возвращает случайное значение целочисленного типа на промежутке от нуля до аргумента, не включая аргумент. Таким образом случайное число на промежутке [a; b] можно сгенерировать, вычислив сумму a + random (b - a).
Задача: Найти разность произведения и суммы цифр случайного целого положительного трёхзначного целого числа.
Программа начинается со служебного слова program. Назовём нашу программу cifry. Напишем раздел описания переменных. Для работы программы нам их потребуется четыре. Это непосредственно число, зовём её c. Так же нам потребуются переменные для хранения суммы и произведения цифр числа. Назовём их соответственно s и p. По условию задачи все они – целые числа – укажем их тип integer. Ещё нам понадобится переменная для хранения одной из цифр числа, назовём её d. Для хранения одной цифры нам будет достаточно типа byte.
Запишем логические скобки. В начале с помощью оператора writeln выведем на экран поясняющее сообщение о том, что это программа расчёта разности произведения и суммы цифр трёхзначного числа. Сгенерируем случайное целое трёхзначное число. Но как это сделать? Для этого присвоим переменной с значение суммы числа 100 и случайного числа от 0 до 899, которое сгенерируем оператором random (900). Эта сумма будет в любом случае иметь три знака, так как её минимальное значение равно 100, а максимальное – 999. Теперь с помощью оператора writeln выведем на экран поясняющее сообщение и само число.
Теперь мы будем вычислять значения суммы и произведения цифр числа. Для этого переменной p присвоим значение 1, а s – 0. В дальнейшем переменную p будем умножать на значения цифр числа, а переменную s – увеличивать на это же значение. Теперь подумаем, как можно выделить одну из цифр числа, допустим наименьшую по разряду. Эта цифра будет равна остатку от деления числа на 10. Присвоим это значение переменной d. Операция нахождения остатка от деления записывается словом mod. Увеличим на значение d переменную s. Теперь умножим переменную p на d. Присвоим результат ей же. Теперь у переменной c нужно отбросить наименьшую по разряду цифру. Для этого достаточно разделить её значение без остатка на 10. Операция безостаточного деления записывается словом div. Для того чтобы выделить следующую цифру числа, достаточно точно также, как и в случае с первой цифрой, воспользоваться функцией нахождения остатка от деления на 10. Просто скопируем и вставим последние четыре оператора. Тоже самое сделаем и для последней цифры числа. Снова вставим последние четыре скопированных оператора.
Таким образом мы вычислили значения произведения и суммы цифр числа. Нам остаётся вывести значение их разности. Используем для этого оператор write. Сначала выведем поясняющее сообщение о том, что это разность произведения и суммы цифр числа, а потом и само значение разности (p - s).
program cifry;
var
c, s, p: integer;
d: byte;
begin
writeln ('Программа расчёта разности произведения и суммы цифр трёхзначного числа.');
c:=100+random (900);
writeln ('Число - ', c);
p:=1;
s:=0;
d:=c mod 10;
s:=s+d;
p:=p*d;
c:=c div 10;
d:=c mod 10;
s:=s+d;
p:=p*d;
c:=c div 10;
d:=c mod 10;
s:=s+d;
p:=p*d;
c:=c div 10;
write ('Разность произведения и суммы цифр числа - ', p-s);
end.
Исходный код программы
Запустим программу на выполнение. Программа сгенерировала число 344. Разность произведения и суммы его цифр действительно равна 37.

Результат работы программы
Важно запомнить:
· Линейный алгоритм – это алгоритм, в котором используется лишь один тип конструкции – следование. Он состоит из операторов, записанных в порядке их выполнения.
· Возможно неявное преобразование значений целочисленных типов byte и integer в вещественный тип real, но не наоборот.
· Для всех числовых типов определён ряд операций и функций над ними.
· Также определены отдельные операции и функции для целочисленных типов: byte и integer, а также для вещественного типа real.

 Получите свидетельство
Получите свидетельство Вход
Вход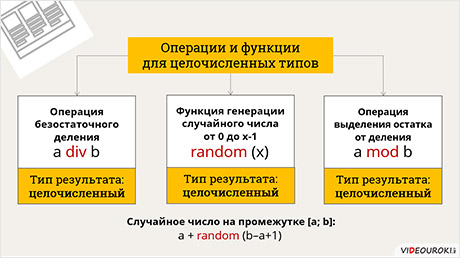



 2
2 5754
5754


Здравствуйте, Татьяна. Благодарим Вас за внимание к нашим проектам. Пришлите, пожалуйста, в нашу службу техподдержки на email: [email protected] ссылку на данное видео, которое размещено в свободном доступе.
Не могу понять. На youtube это же видео в свободном доступе. Почему на родном сайте закрыт доступ?