Сегодня на уроке мы напомним, какие соединения называют сочетаниями. Вспомним формулу для подсчёта числа сочетаний, а также свойства сочетаний. Познакомимся с формулой бинома Ньютона. Скажем, что называют треугольником Паскаля. Познакомимся со свойством элементов строки треугольника Паскаля.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним,
что сочетаниями из  элементов
по
элементов
по  элементов в каждом (
элементов в каждом ( ) называются
соединения, каждое из которых содержит
) называются
соединения, каждое из которых содержит  элементов,
взятых из данных
элементов,
взятых из данных  разных
элементов, и которые отличаются одно от другого по крайней мере одним
элементом.
разных
элементов, и которые отличаются одно от другого по крайней мере одним
элементом.
Формула для подсчёта числа сочетаний из  различных
элементов по
различных
элементов по  элементов в каждом имеет вид
элементов в каждом имеет вид  .
.
Также данную формулу можно представить в виде  .
.
Напомним два свойства сочетаний, которые в ряде случаев упрощают вычисления при решении задач.
Свойство первое:  .
.
Свойство второе:  .
.
С сочетаниями тесно связана формула бинома Ньютона, с которой мы сегодня познакомимся.
Биномами в теории многочленов часто называют двучлены. Давайте с
вами рассмотрим целые неотрицательные степени бинома  при условии,
что
при условии,
что  .
.

Мы можем продолжить возводить бином  в шестую, седьмую и так далее степени. Но
давайте обратим внимание, что эти формулы мы можем записать следующим образом:
в шестую, седьмую и так далее степени. Но
давайте обратим внимание, что эти формулы мы можем записать следующим образом:

Эту формулу часто называют просто Биномом Ньютона. Она
справедлива для каждого натурального значения  . Числа
. Числа  называют биномиальными коэффициентами,
которые могут быть найдены по формуле
называют биномиальными коэффициентами,
которые могут быть найдены по формуле  .
.
Давайте, пользуясь этой формулой возведём бином  в шестую
степень.
в шестую
степень.


Вообще, биномиальные коэффициенты легко находить с помощью так называемого треугольника Паскаля.
Треугольник Паскаля – таблица
значений  , которая
составлена на основе рекуррентного свойства числа сочетаний
, которая
составлена на основе рекуррентного свойства числа сочетаний  с учётом того, что
с учётом того, что  .
.
Сейчас вы видите фрагмент треугольника Паскаля, в котором показан процесс получения определённых членов таблицы на основании рекуррентного свойства сочетаний.

Отметим, что треугольник Паскаля можно продолжать как угодно далеко.
Данная таблица наглядно иллюстрирует известное нам первое свойство сочетаний. Его можно сформулировать так: числа, одинаково удалённые от концов строки треугольника Паскаля, равны.
Теперь запишем разложение бинома  .
.

Обратите внимание, что показатель степени данного бинома равен пяти. А число членов полученного многочлена равно шести, то есть на единицу больше.
Показатели степени первого слагаемого, то есть  ,
последовательно убывают на единицу от
,
последовательно убывают на единицу от  до
до  , а
показатели степени второго слагаемого, то есть
, а
показатели степени второго слагаемого, то есть  , возрастают
на единицу от
, возрастают
на единицу от  до
до  .
.
Кроме этого заметим, что биномиальные коэффициенты, которые одинаково удалены от начала и от конца разложения, равны между собой.
Таким образом, при записи разложения степени бинома полезно контролировать следующие моменты:
1) число членов получаемого многочлена на единицу больше
показателя ЭМ степени бинома, то есть равно  ;
;
2) показатели степени первого слагаемого бинома последовательно
убывают на единицу от  до
до  , а
показатели второго последовательно возрастают на единицу от
, а
показатели второго последовательно возрастают на единицу от  до
до  ;
;
3) биномиальные коэффициенты, равноудалённые от начала и конца разложения по формуле бинома Ньютона, равны между собой.
Сейчас вы видите свойство элементов строки треугольника Паскаля:
 .
.
Это равенство получается из формулы бинома Ньютона при  .
.
Действительно, подставим в формулу 1 вместо  и
и  . Выполним
преобразование и получим данное свойство.
. Выполним
преобразование и получим данное свойство.

А теперь выполним несколько заданий.
Задание первое. Запишите разложение
бинома  .
.
Решение.

Задание второе. С помощью свойства элементов строки треугольника Паскаля найдите суммы:
а)  ; б)
; б)  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход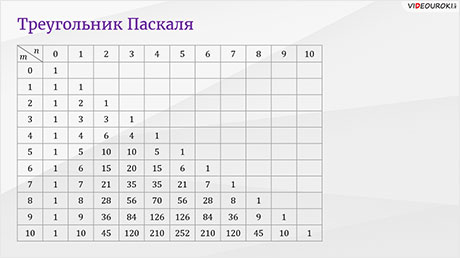




 3893
3893