Величины, характеризующие КД. Гармонические колебания

На прошлом уроке мы познакомились с новым видом механического движения — колебательным. Давайте вспомним, что это движение, при котором состояния тела с течением времени повторяются, при этом тело проходит через положение устойчивого равновесия поочерёдно в противоположных направлениях. Причём, если колебания происходят в системе только под действием внутренних сил, то такие колебания называются свободными.

А ещё мы дали определение маятника. Напомним, что это твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

На рисунке вы видите два колеблющихся нитяных маятника. Чем они отличаются?

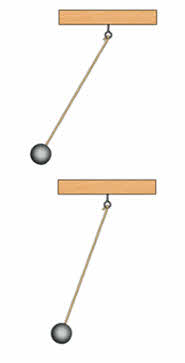
Правильно, верхний маятник колеблется с большим размахом, чем нижний.

В физике наибольшее по модулю отклонение колеблющегося тела от положения равновесия называют амплитудой колебаний.

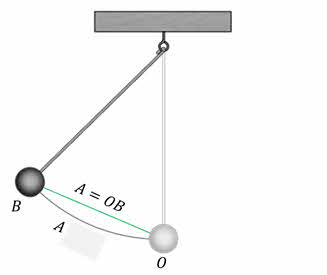
Она зависит только от того, на сколько тело было отведено от положения равновесия перед тем, как его предоставили самому себе. Обозначается амплитуда большой буквой А. Единицей её измерения в СИ является метр.

Мы с вами будем изучать колебания, амплитуда которых мала, то есть когда длину дуги ОВ можно считать равной длине отрезка ОВ.

На прошлом уроке мы с вами ввели в рассмотрения величину, называемую периодом колебаний. Напомним, что это промежуток времени, в течение которого тело совершает одно полное колебание. Иными словами, это время, за которое колеблющееся тело проходит путь, равный четырём амплитудам:

По аналогии с вращательным движением, число колебаний в единицу времени называется частотой колебаний. За единицу частоты в СИ принято одно колебание в секунду. Эта единица называется герцем, в честь немецкого учёного Генриха Герца, с трудами которого вы познакомитесь в старших классах.

Как и при движении тела по окружности, период колебаний и частота связаны между собой обратной пропорциональностью.

Продолжим рассматривать колебания нитяного маятника. Давайте проведём эксперимент, который покажет, зависит ли его период колебаний от амплитуды? Для этого возьмём три маятника с одинаковыми длинами нитей и грузами одной массы, но запустим каждый маятник с разного расстояния относительно положения равновесия.

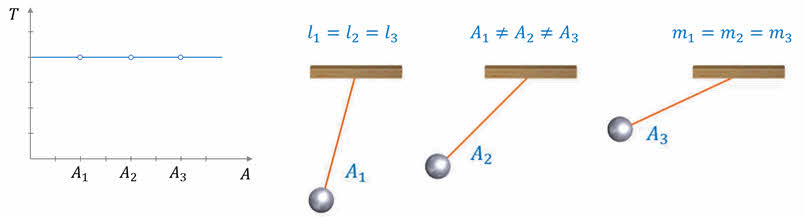
Не трудно заметить, что период колебаний нитяного маятника не зависит от амплитуды.

Теперь посмотрим, зависит ли период колебаний от массы маятника. Опять рассмотрим три маятника с одинаковыми длинами нитей, но с разными массами грузов.

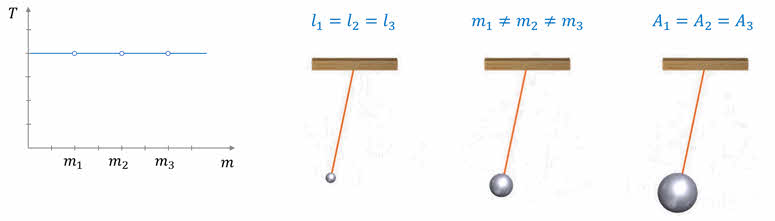
Из опыта видно, что все три маятника имеют одинаковые периоды колебаний, то есть период колебаний не зависит от массы груза.

И, наконец, проверим, зависит ли период колебаний маятника от длины его нити. Для этого возьмём три маятника с одинаковыми массами грузов, но с разными длинами нитей.

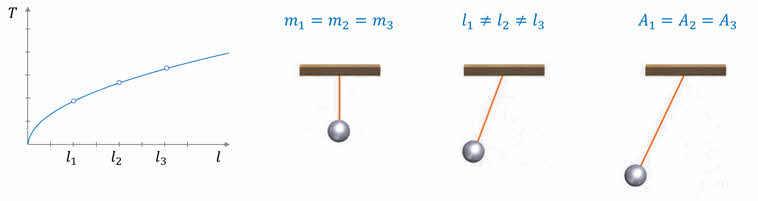
Колебания маятников наглядно нам демонстрируют, что их период зависит от длины нити маятника: чем длиннее нить, тем больше период колебаний и меньше частота.

Свободные колебания, происходящие при отсутствии трения и сопротивления воздуха, называются собственными колебаниями, а их частота — собственной частотой колебательной системы.

Не только нитяной маятник, но и любая другая колебательная система имеет определённую собственную частоту, которая будет зависеть от параметров колебательной системы.

Например, нетрудно показать, что период колебаний пружинного маятника зависит от массы груза и жёсткости пружины.

Теперь давайте рассмотрим колебания двух абсолютно одинаковых нитяных маятника. Выведем их из положения равновесия, отклонив верхний маятник на некоторый угол влево, а нижний — на такой же угол, но вправо, и отпустим их. Итак, оба маятника колеблются с одинаковым периодом (так как длины их нитей равны) и с одинаковыми амплитудами. Но в любой момент времени скорости маятников направлены в противоположные стороны. В этом случае говорят, что маятники колеблются в противофазе друг с другом.

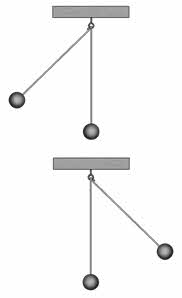
Повторим опыт, но теперь отклоним маятники в одну сторону на один и тот же угол. Маятники вновь колеблются с одинаковыми частотами, но теперь их скорости в каждый момент времени направлены одинаково. Говорят, что такие маятники колеблются в одинаковых фазах (или синфазно).

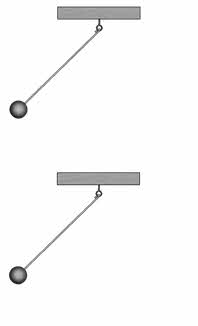
И последний случай. В момент начала наблюдения скорости обоих маятников сонаправлены. Однако через небольшой промежуток времени скорости маятников направлены в противоположные стороны. В таком случае говорят, что колебания маятников происходят с определённой разностью фаз.

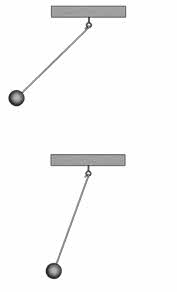
Таким образом, фаза колебаний — это физическая величина, которая показывает, на сколько колебания одного маятника отстают или опережают колебания другого маятника. Это определение, конечно, не очень строгое, но для понимания сути величины, вполне достаточное.

Таким образом, любой колебательное движение характеризуется тремя величинами:

·                   амплитудой колебаний;

·                   периодом колебаний (или частотой);

·                   фазой колебаний.

Простейшим видом колебательного движения являются гармонические колебания. Термин «гармонические колебания» впервые был введён в науку швейцарским физиком Даниилом Бернулли.

Итак, гармоническими называются такие колебания, которые происходят под действием силы, пропорциональной смещению колеблющегося тела и направленной противоположно этому смещению.

При определённых условиях примером гармонических колебаний будут служить колебания пружинного маятника.

Установим графическую зависимость смещения колеблющегося тела от времени. Для этого проведём такой опыт. Прикрепим к пружинному маятнику грифель от карандаша, а за маятником расположим бумажную ленту и будем равномерно её тянуть. На ленте мы увидим линию, которая по форме будет совпадать с графиком колебаний.

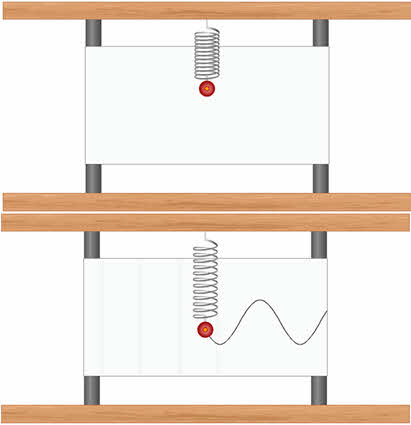
График колебаний математического маятника можно получить, проведя аналогичный опыт. Маятником здесь служит воронка с песком. Если под колеблющимся маятником равномерно тянуть бумажную ленту, перпендикулярно плоскости колебаний, то на ней останется волнообразная дорожка из песка. Каждая точка этой дорожки соответствует положению маятника в тот момент, когда он проходил над ней.

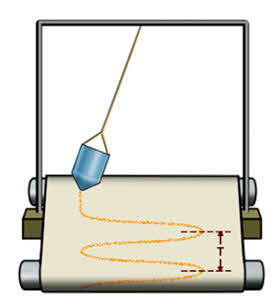
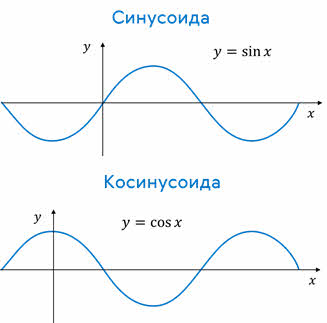
Из результатов двух опытов мы видим, что след, который оставляет песок или карандаш на листе бумаги, есть некая волнообразная кривая. Её называют синусоидой. Из курса математики старших классов вы узнаете, что такие же графики имеют функции типа:

Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.

Если провести ось времени через точки, соответствующие положению равновесия маятника, а перпендикулярно ей — ось смещения, то по графику колебаний можно определить все характеристики колебательного движения. Так, максимальные отклонения маятника от положения равновесия в обе стороны одинаковы по модулю и равны А — это амплитуда колебания. А расстояние между двумя пиками графика — период колебаний.

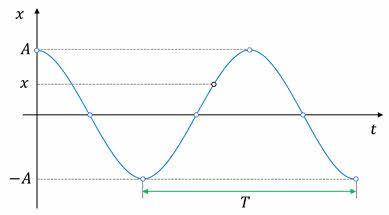
То есть смотрите, маятник начал движение из крайней точки с координатой А. Затем, пройдя положение равновесия, дошёл до второй крайней точки с координатой –А, на мгновение остановился в ней, поменяв направление скорости на противоположное, а затем продолжил движение в обратном направлении и, вновь пройдя через положение равновесия, вернулся туда, откуда начал движение. Затем движение маятника повторяется.

Так же с помощью данного графика можно примерно определить координату маятника в любой момент времени.

Теперь мы можем дать более строгое определение гармонических колебаний. Итак, гармоническими колебаниями называются периодические изменения во времени физической величины, происходящие по закону синуса или косинуса.

Рассмотренные нами колебания нитяного маятника близки к гармоническим, но не являются таковыми, из-за действия различных сил сопротивления. Но если бы маятник представлял собой материальную точку, колеблющуюся без трения с малой амплитудой при неизменном расстоянии от неё до точки подвеса, то его колебания были бы строго гармоническими. Такая колебательная система называется математическим маятником.

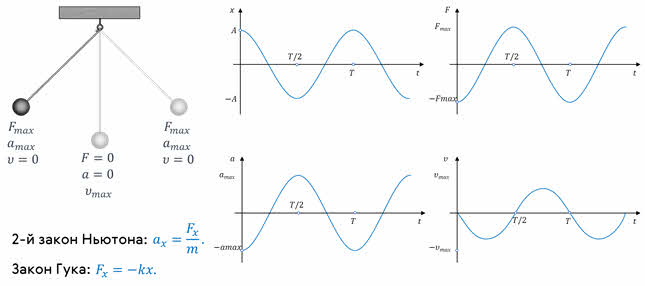
Следует помнить, что при совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение и скорость тоже изменяются по закону синуса или косинуса. Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.

Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.