Закон сохранения энергии в механике

На одном из прошлых уроков мы с вами показали, какое важное значение в физике имеет импульс тела, для которого существует закон сохранения. Не менее важную роль не только в физике, но и во всех отраслях науки и техники, играет и другая физическая величина — энергия. Мы с вами уже познакомились с понятием механической энергии. Давайте с вами вспомним, что это физическая величина, являющаяся функцией состояния системы и характеризующая её способность совершать работу.

В механике принято различать два вида механической энергии: кинетическую и потенциальную.

Конечно же, любое тело может обладать двумя видами механической энергии одновременно. Но вот вопрос, могут ли измениться и кинетическая и потенциальная энергии одновременно? Давайте с вами рассмотрим простую систему тел, состоящую из Земли и мяча.

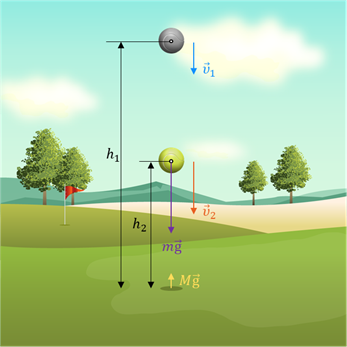
Будем считать, что мяч свободно падает и на некоторой высоте h₁ его скорость равнялась υ₁, а на высоте h₂ — увеличилась до υ₂. Так как мяч находится в свободном падении, то на него действует только сила тяжести со стороны Земли, которая будет совершать работу по его перемещению с одного уровня на другой. С одной стороны, эта работа равна изменению потенциальной энергии мяча, взятой с обратным знаком:

𝐴 = –ΔЕ_п.

А с другой стороны (так как меняется скорость мяча), эту же работу можно найти на основании теоремы об изменении кинетической энергии: 

𝐴 = ΔЕ_к.

Обратим внимание на то, что работу силы тяжести, действующей на Землю со стороны камня, мы не учитываем, так как она практически равна нулю из-за огромной массы нашей планеты.

Таким образом, мы с вами получаем два уравнения для нахождения одной и той же физической величины — работы силы тяжести. Поэтому мы можем приравнять их правые части:

–ΔE_п = ΔE_к

Из полученного равенства видно: при свободном падении мяча его потенциальная энергия уменьшалась ровно на столько, на сколько увеличивалась энергия кинетическая. Отсюда следует, что изменение суммы кинетической и потенциальной энергий равно нулю:

Δ(E_п + E_к) = 0.

Сумма кинетической и потенциальной энергий тел, входящих в систему, называется полной механической энергией системы:

Е = E_п + E_к = const.

Таким образом, в замкнутой системе тел, взаимодействующих консервативными силами, механическая энергия остаётся неизменной.

Это утверждение называется законом сохранения энергии в механике.

А теперь давайте с вами рассмотрим такой опыт. Вот на столе лежит обычный деревянный брусок. Действующие на него внешние сила тяжести и сила нормальной реакции со стороны стола компенсируют друг друга.

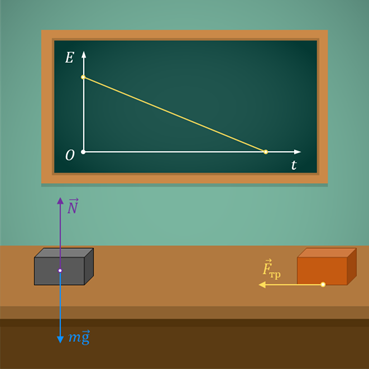
Теперь толкнём брусок, придав ему некоторую начальную скорость. Он придёт в движение и, пройдя некоторое расстояние, остановится из-за действия на него силы трения. И, несмотря на то, что внешние силы работы не совершали, полная механическая энергия системы уменьшилась.

Таким образом, если в замкнутой системе между телами действует сила трения, то полная механическая энергия убывает. Причём изменение механической энергии равно работе силы трения:

ΔE = А_тр.

Отличие сил трения от консервативных сил можно рассмотреть и на таком примере. Пусть мячик падает с некоторой высоты h и после абсолютно упругого соударения с полом отскакивает на такую же высоту. Чему равна работа силы тяжести, действующей на мяч, в этом примере?

Правильно, нулю, так как траекторией полёта мяча была замкнутая линия. При этом во время движении мяча вниз сила тяжести совершала положительную работу, а при движении вверх — отрицательную. А вот работа силы сопротивления воздуха была отрицательна на всём пути мяча: и при движении вверх, и при движении вниз. Поэтому на замкнутой траектории работа силы сопротивления воздуха отлична от нуля.

Силы, работа которых зависит от формы траектории точки приложения силы и на замкнутой траектории не равна нулю, называются неконсервативными или диссипативными силами.

Таким образом, в системе, в которой действуют неконсервативные силы, полная механическая энергия не сохраняется. Не сохраняется она и тогда, когда в системе тел происходят неупругие деформации. Но уменьшение механической энергии не означает, что она бесследно исчезла. Она лишь переходит из механической формы в другие и, в частности, во внутреннюю энергию.

Впервые на эту особенность обратил внимание Роберт Майер в 1841 году. А в 1847 году немецкий физик Герман фон Гельмгольц сформулировал один из фундаментальных законов природы — закон сохранения энергии. В современной формулировке он звучит так: величина полной энергии замкнутой системы остаётся постоянной. При этом энергия не создаётся и не уничтожается, она лишь переходит из одной формы в другую.

Этот закон не знает исключений. Он выполняется для всех физических, химических, биологических и других явлений.

Для закрепления материала решим с вами задачу. Тело брошено вверх с начальной скоростью 20 м/с. Если за нулевой уровень потенциальной энергии принять поверхность Земли, то на какой высоте кинетическая энергия тела будет равна его потенциальной энергии? Сопротивлением воздуха можно пренебречь, а ускорение свободного падения принять равным 10 м/с².

При решении данной задачи систему тело — Земля будем считать изолированной.