Измерение ускорения бруска при движении по наклонной плоскости

Цель этой работы: с помощью экспериментальной установки определить ускорение скольжения бруска по наклонной плоскости.

Для выполнения этой работы мы будем использовать оборудование из комплекта № 5 в составе: штатив с креплением для наклонной плоскости, направляющая со шкалой, деревянный брусок с пусковым магнитом, электронный секундомер с датчиками, линейка и транспортир.

Прежде чем приступить к работе давайте с вами вспомним, что неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения.

Из всех видов неравномерного движения в школе изучают самое простое — прямолинейное равноускоренное движение. Так называют движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.

Для того, чтобы описать насколько быстро меняется скорость тела, в физике ввели величину, которую назвали ускорением тела. Ускорение — это физическая векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:

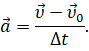
Именно ускорение тела нам и предстоит определить в данной работе. Однако очевидно, что данная формула нам не подходит, так как в ней фигурирует скорость тела, измерить которую прямыми измерения в классе мы не можем. А анализ оборудования нам говорит о том, что для определения ускорения мы с вами должны воспользоваться формулой, для определения перемещения тела при его равноускоренном движении:

Так как мы будем изучать прямолинейное равноускоренное движение без начальной скорости при котором направление векторов перемещения и ускорения совпадают, то мы с вами можем записать, что модуль вектора перемещения прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено:

Отсюда, зная пройденный телом путь и время его движения, мы с вами легко можем определить модуль ускорения, с которым двигалось тело:

Теперь приступим к выполнению работы. Итак, для начала давайте соберём экспериментальную установку. Для этого на штативе закрепим наклонную плоскость. После этого, используя транспортир, установим направляющую под углом 45° к поверхности стола.

Далее установим на направляющей датчики секундомера: первый расположим в точке 0, а второй — в точке 40 см. При пуске бруска пусковой магнит мы установим на пол сантиметра выше первого датчика.

Далее мы сделаем рисунок нашей установки. Для этого схематически изобразим штатив с прикреплённой к нему направляющей. На направляющей расположим брусок так, как это показано на экране. Также на рисунке мы должны будем указать перемещение тела и направление вектора ускорения. Не лишним будет показать и угол, под которым установлена направляющая.

Запишем формулы, которыми будем пользоваться при выполнении данной работы. Как мы уже вспоминали, при прямолинейном равноускоренном движении без начальной скорости при котором направление векторов перемещения и ускорения совпадают, модуль вектора перемещения (путь) прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено:

С формулами разобрались, теперь запишем результат измерения пути, пройденного бруском, с учётом абсолютной погрешности измерения (путь нам дан в условии задания):

Теперь приступим непосредственно к выполнению работы. Итак, подключаем электронные датчики к секундомеру, а брусок устанавливаем так, чтобы пусковой магнит находился на пол сантиметра выше первого датчика. Отпускаем брусок.

Значение промежутка времени, за которое брусок преодолел заданный отрезок пути, записываем в бланке ответов с учётом погрешности измерения:

Опыт повторяем ещё два раза, каждый раз записывая результаты измерений.

Прямы измерения мы с вами завершили. Теперь давайте определим среднее значение промежутка времени, как среднее арифметическое значение всех трёх опытов:

Найденное среднее значение времени мы должны записать также с учётом погрешности измерения:

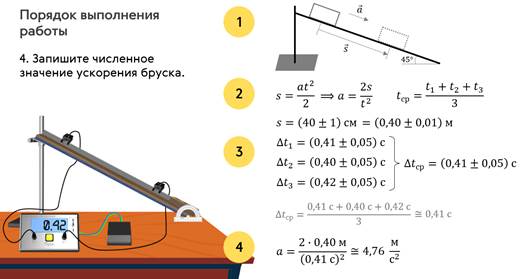
И, наконец, мы определяем ускорение бруска. Для чего в расчётную формулу подставляем значения пути и среднего времени движения бруска на этом отрезке пути:

В выводе напишем: ускорение бруска при его движении по наклонной плоскости равно 4,76 м/с².