Запись вспомогательных алгоритмов на языке Паскаль. Функции

На прошлых уроках мы узнали метод последовательного конструирования алгоритмов, при котором задача последовательно разбивается на подзадачи, пока они не станут понятны исполнителю. А также, что некоторые подзадачи бывает удобно оформить в виде вспомогательных алгоритмов, которые целиком используются в составе других. Вспомогательные алгоритмы в языке Pascal записываются в виде именованных последовательностей команд, которые называются подпрограммами. Подпрограммы делятся на процедуры и функции.

Вопросы:

·      Что такое функция?

·      Чем отличается функция от процедуры

·      Как записывается функция?

·      При решении каких задач можно применять функции?

И так, ещё одним видом подпрограмм, помимо процедур, являются функции. Функцией называется подпрограмма, возвращающая всего одно значение. Оно сохраняется в ячейке памяти с именем, которое совпадает с названием функции. То есть функция принимает на вход несколько или одну переменную, а по выполнении команд возвращает всего одну переменную, с именем, которое совпадает с названием функции, в отличие от процедуры, которая может возвращать несколько переменных.

Схема работы функции

Запись функции в программе похожа на запись процедуры. Функции записываются между разделом описания переменных и телом основной программы в любом удобном порядке. В начале, записывается служебное слово function, после которого идёт имя функции. Оно, как имя процедуры не должно совпадать с именем программы или переменных. Оно может содержать несколько цифр, букв латинского алфавита или знаков подчёркивания. И может начинаться с буквы латинского алфавита или знака подчёркивания. Далее в круглых скобках, следует перечисление входных параметров с указанием типов. После скобок следует двоеточие и тип возвращаемого значения, после которого ставится точка с запятой. Затем, если в процессе работы функции нужны промежуточные переменные, как и при записи процедуры, следует раздел описания переменных функции. Названия переменных и параметров функции могут совпадать с именами переменных в основной программе или других функциях, поэтому их стоит выбирать для решения данной подзадачи.

Затем между служебными словами begin и end следует тело функции. Так как значение возвращаемое функцией сохраняется в переменную, название которой совпадает с её названием, тело функции должно содержать хотя бы одну команду присваивания переменной с этим названием какого либо значения. Как и при записи процедуры после служебного слова end следует точка с запятой.

Схематичная запись функции

Вызов функции отличается от вызова процедуры. Если процедура вызывается как отдельная команда в составе основного алгоритма, то вызов функции происходит в составе другой команды или оператора. При этом функция записывается как один из параметров оператора. После имени функции в круглы скобках, как и при записи процедуры задаются её входные параметры, в качестве которых могут быть заданы как переменные, так и константы. Так, как функция имеет один выходной параметр с названием, совпадающим с названием функции, в отличии от процедуры, выходные параметры в круглых скобках не перечисляются. Так же как и при записи процедуры, при перечислении параметров стоит соблюдать их порядок следования и совместимость типов.

Схематичный приме вызова функции

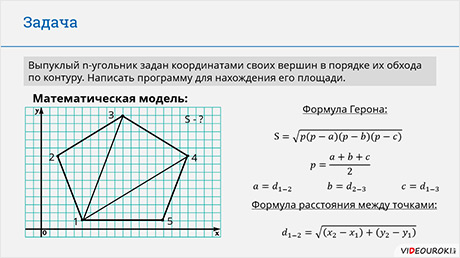
Задача: Выпуклый n-угольник задан координатами своих вершин в порядке их обхода по контуру. Написать программу для вычисления его площади.

Составим математическую модель. Мы еще не знаем как найти площадь выпуклого многоугольника, поэтому разобъем его на отдельные треугольники, проведя из его первой вершины отрезки к остальным. Таким образом у нас получится n - 2 треугольника, площади которых мы уже можем найти. Вспомним что площадь треугольника можно найти, воспользовавшись формулой Герона,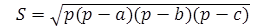, где a, b и c – длины сторон треугольника, а p – его полупериметр.

Для того, чтобы воспользоваться формулой Герона для вычисления площади треугольника, нам необходимо знать длины его сторон. Они равны расстояниям между вершинами треугольника. Вспомним что расстояние между двумя точками на координатной плоскости можно найти, по следующей формуле 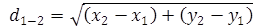, где x и y – координаты соответствующих точек.

Математическая модель решения задачи

Составим блок-схему алгоритма решения задачи. Обозначим в ней x - массив координат x вершин, у - массив координат y, n - количество вершин многоугольника, i - номер текущей вершины, r - площадь n-угольника, а так же мы используем вспомогательные алгоритмы d - нахождения расстояния между двумя точками на координатной плоскости и s - нахождения площади треугольника по формуле Герона.

Вначале мы должны считать значение n, после чего запишем цикл «для i от 1 до n», в котором будет команда считывания координат i-той вершины n-угольника. Так, как наш алгоритм будет сводится к расчёту суммы площадей треугольника, как и в алгоритме нахождения суммы элементов массива присвоим переменной r значение 0. Далее будет следовать цикл вычисления площади n-угольника. Мы разобъем его на треугольники, координатами вершин которых будут вершины n-угольника с номерами 1, так, как из этой вершины мы проводили разделительные отрезки, а так же любые две соседние вершины с номерами i и i + 1. Так мы запишем цикл «для i от 2 до n - 1». Он будет содержать всего одну команду, увеличения переменной r на значение площади очередного треугольника, то есть r:=r+s(…). В качестве входных параметров для функции s() будут длины сторон треугольника, которые, мы вычислим с использованием вспомогательного алгоритма d(), его параметрами в первом случае будут координаты первой и i-той вершин, во втором – i-той и i + 1, а в третьем - первой и i + 1. В конце нам останется лишь вывести значение переменной r.

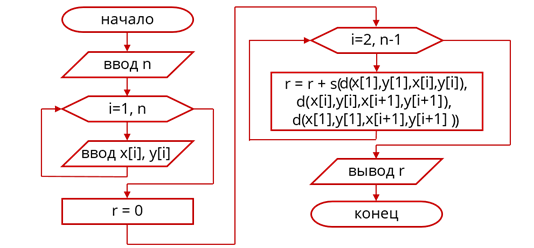
Блок-схема алгоритма решения задачи

Запишем программу по данной блок-схеме. Назовём её area, что в переводе с английского языка означает площадь. По смыслу задачи координаты точек и значение площади могут быть дробными числами. То есть нам понадобится два массива, x и y из 100 элементов типа real. Обратим внимание что запись массива вещественных чисел отличается от записи массива целых чисел лишь типом элементов. Ещё нам понадобится переменная r так же типа real. И переменные n и i типа integer.

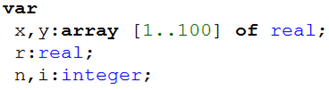
Раздел описания переменных программы

Между служебными словами begin и end запишем тело программы. Выведем поясняющее сообщение о том, что это программа расчета площади многоугольника и запрос на ввод количества вершин. Теперь запишем команду считывания n. Запишем цикл for i:=1 to n do, который будет содержать команду вывода на экран запроса на ввод координат i-той вершины, а так же команду их считывания.

Теперь запишем команду присваивания переменной r значения 0 и цикл вычисления площади многоугольника. Это будет цикл for i:=2 to n-1 do. Он будет содержать всего одну команду увеличения числа r на значение площади треугольника с вершинами, которые будут вершинами многоугольника с номерами 1, i и i + 1. Для этого в составе оператора суммы его параметром будет указано значение функции вычисления площади треугольника s(), которую мы оформим позже, она будет принимать на вход длины сторон треугольника, которые мы найдем с помощью функции расчета расстояния между двумя точками на координатной плоскости. В первом случае её параметрами будут координаты вершин с номерами 1 и i, во втором - i и i + 1 и в третьем 1 и i + 1.

Теперь нам остается лишь вывести поясняющее сообщение с текстом «Площадь заданного треугольника равна», и значение переменной r.

Тело основной программы

Оформим функции для нашей программы. Начнем с функции нахождения расстояния между двумя точками. Запишем служебное слово function, и название функции d. Она будет принимать на вход координаты двух точек x1, y1 и x2, y2 все типа real. Данная функция будет возвращать значение расстояния между двумя точками, которое может быть дробным, то есть тип возвращаемого значения будет real. Промежуточных переменных в данной функции не потребуется. Между служебными словами begin и end запишем тело функции. Оно будет содержать только одну команду, присваивание переменной d значения расстояния между двумя точками, которое рассчитано по формуле из математической модели. Функция извлечения квадратного корня, на языке Паскаль, записывается командой sqrt, после которой в круглых скобках указывается число или выражение из которого требуется извлечь квадратный корень.

Код функции вычисления расстояния между двумя точками

Теперь напишем функцию нахождения площади треугольника по формуле Герона. Запишем служебное слово function и название функции s. Входными параметрами будут значения длин сторон треугольника: a, b и c типа real. Возвращаемое значение, площадь треугольника, может быть дробной, поэтому оно тоже будет типа real. В этой функции нам понадобится промежуточная переменная p типа real, которая будет хранить значение полупериметра треугольника. Запишем тело функции, она будет содержать команду вычисления полупериметра. Для этого достаточно найти сумму длин сторон треугольника и разделить её пополам, а также команду присваивания переменной s площади треугольника, рассчитанной по формуле Герона.

Код функции вычисления площади треугольника

Придумаем несколько тестов для программы. В качестве многоугольника зададим прямоугольник с координатами вершин: 0; 0, 0; 4, 8; 4 и 8; 0. Для себя площадь данного прямоугольника можно рассчитать, умножив его длину на ширину. 8 * 3 = 32.

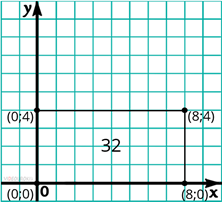
Прямоугольник из первого теста

Придумаем ещё один тест. Для этого достаточно к прямоугольнику из прошлого теста дорисовать равнобедренный треугольник сверху, координаты его боковых вершин будут совпадать с координатами верхних вершин прямоугольника, а верхняя вершина будет находиться в точке с координатами 4; 7. Площадь добавленного треугольника мы можем рассчитать по формуле площади равнобедренного треугольника, умножив его высоту 3, на половину основания 4, его площадь равна 12. Добавим к этому результату площадь прямоугольника и получим, площадь получившегося пятиугольника равной 44.

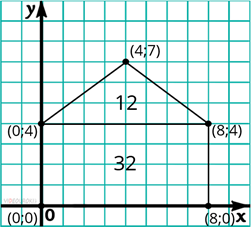
Пятиугольник из второго теста

Введем данные из первого теста в программу. Программа вывела что площадь заданного многоугольника равна тридцати двум, данный результат соответствует ожидаемому.

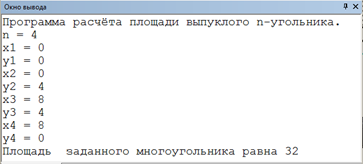
Результат работы программы по первому тесту

Введем данные из второго теста в программу. Программа вывела что площадь заданного многоугольника равна сорока четырем, данный результат соответствует ожидаемому. Так, как результаты работы программы в обоих тестах соответствуют ожидаемым – задача решена верно.

Результат работы программы по второму тесту

Важно запомнить:

·      Функцией называется подпрограмма, возвращающая всего одно значение, которое записывается в переменную с именем, совпадающим с именем функции.

Мы научились оформлять вспомогательные алгоритмы в виде функций и использовать их при решении задач.