Вывод закона сохранения механической энергии

На прошлых уроках мы с вами видели, какое важное значение имеет импульс тела, для которого существует закон сохранения. Столь же большую играет и другая величина, которая для замкнутой системы тоже остаётся постоянной. Эта величина — энергия, с которой приходится иметь дело не только в механике, но и в других разделах физики, во всех науках о природе, во всех отраслях техники, да и в повседневной жизни. Подобно тому, как одна величина — импульс тела, связана с другой величиной — импульсом силы, энергия тоже связана с другой величиной — работой силы, или механической работой.

С понятиями механическая работа и энергия мы с вами знакомились в седьмом классе. Давайте вспомним, работой называется скалярная физическая величина, численно равная произведению модуля силы на модуль перемещения тела.

А механическая энергия — это физическая величина, характеризующая способность системы совершать работу.

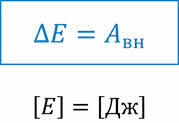
В механике принято различать два вида механической энергии: кинетическую и потенциальную.

В седьмом классе мы говорили о том, что кинетической энергией обладает любое движущееся тело, и она равна работе, которую нужно совершить, чтобы разогнать тело из состояния покоя до данной скорости.

Также мы с вами говорили о том, что кинетическую энергию можно найти, как половину произведения массы тела на квадрат его скорости.

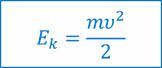
Потенциальная энергия — это энергия взаимодействия тел или частей одного и того же тела. Потенциальная энергия тела, поднятого над землёй, равна работе, которую совершает сила тяжести при перемещении тела на нулевой уровень, который мы вправе выбирать совершенно произвольно.

Конечно же любое тело может обладать как кинетической, так и потенциальной энергией одновременно. Примером может служить летящий самолёт, в системе отсчёта, связанной с Землёй.

Вспомним, что сумма кинетической и потенциальной энергий тела (или системы тел) называется полной механической энергией или просто, механической энергией

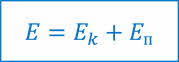
При этом, если система тел является замкнутой, а между телами системы действуют только силы тяготения и силы упругости и отсутствуют силы сопротивления, то её механическая энергия остаётся неизменной.

Иными словами, потенциальная и кинетическая энергия системы могут меняться, превращаясь в друг друга. Но при уменьшении одного вида энергии, на столько же увеличивается энергия другого вида, благодаря чему их сумма и не меняется.

Давайте подтвердим справедливость закона сохранения энергии. Для этого рассмотрим превращения энергии в механической системе на примере свободного падения тела.

Допустим, шарик известной массы падает с некоторой высоты, над поверхностью Земли.

Из полученного равенства видно, при свободном падении шарика его потенциальная энергия уменьшалась ровно на столько, на сколько увеличивалась энергия кинетическая.

Сгруппируем члены уравнения так, чтобы между знаком равенства стояла сумма кинетической и потенциальной энергий в начальном и конечном состояниях:

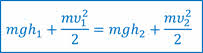
Формула, записанная в таком виде, показывает, что действительно полная механическая энергия шарика при его свободном падении остаётся неизменной.

Это уравнение выражает математическую запись закона сохранения механической энергии.

Таким образом, мы смогли теоретически доказать, что в случае замкнутой системы тел, её полная механическая энергия не меняется с течением времени.

Рассмотрим применение закона сохранения механической энергии для решения задач.

В заключении отметим, что закон сохранения механической энергии является частным случаем всеобщего закона превращения и сохранения энергии.

Энергия не создаётся и не уничтожается, а только превращается из одного вида в другой.

В работе «О сохранении силы» Герман фон Гельмгольц впервые сформулировал и обосновал закон сохранения энергии, отметив его всеобщий характер. Основные свои идеи учёный доложил на заседании Физического общества в 1847 году. Называя кинетическую энергию «живой силой», а потенциальную — «напряжённой силой», Гельмгольц доказывает, что «когда тела природы действуют друг на друга с силами притяжения или отталкивания, независимыми от времени и скорости, то сумма живых и напряжённых сил остаётся постоянной». Так был впервые сформулирован один из самых фундаментальных законов природы — закон сохранения энергии.