Вопросы занятия:
• рассмотреть примеры нахождения площадей фигур, ограниченных различными линиями.
Материал урока
Прежде чем приступить к изучению нового материала, давайте вспомним:

Но с помощью определенного интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида, например, такой
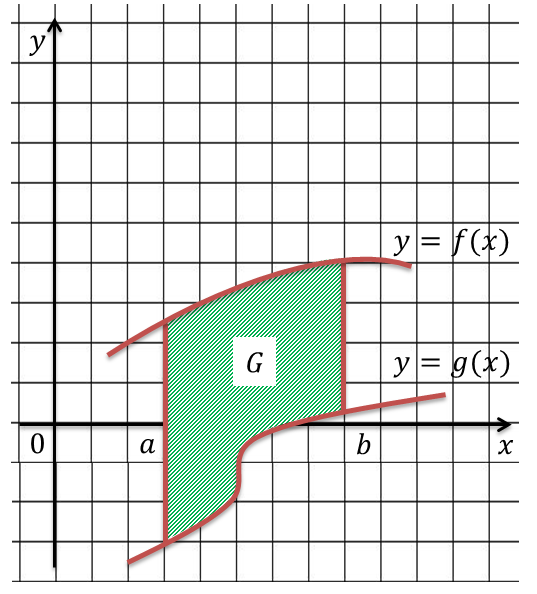
Для того, чтобы вычислить площадь данной фигуры, выполним параллельный перенос фигуры на m единиц вверх так, чтобы она полностью оказалась расположенной в координатной плоскости выше оси абсцисс.
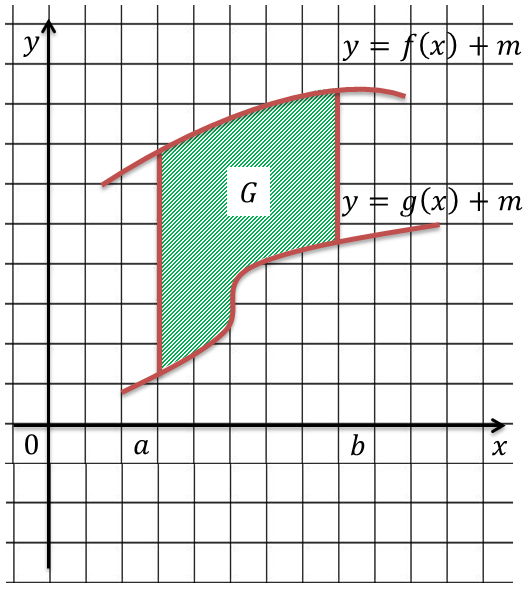
Теперь она ограничена сверху и снизу графиками функции y = f(x) + m и y = g(x) + m, причем обе функции непрерывны и неотрицательны на отрезке [a; b]. Тогда легко заметить, что площадь нашей фигуры можно найти как разность площадей криволинейных трапеций. Запишем это:

Итак:

Рассмотрим пример.
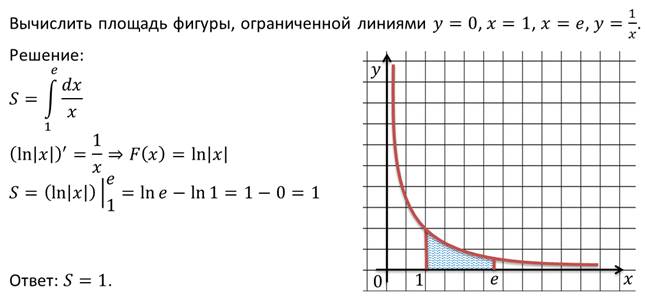
Рассмотрим еще один пример.

Рассмотрим еще один пример.
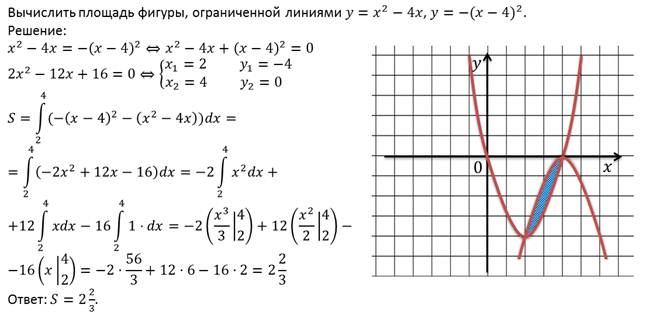
Рассмотрим еще один пример.
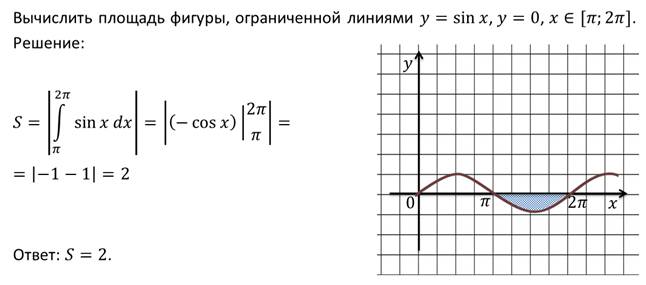
Рассмотрим еще один пример.
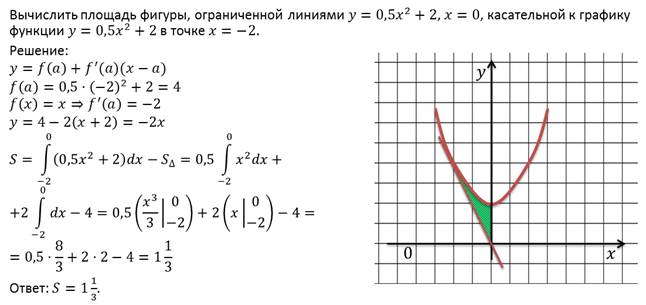

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 5596
5596

