Вопросы занятия:
· рассмотреть функцию y = x2, её свойства и график;
· рассмотреть функцию y = х3, её свойства и график.
Материал урока
На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:
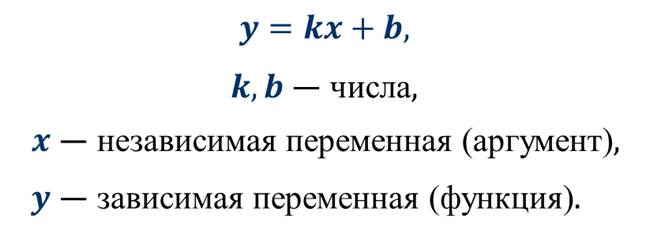
Также вспомним, что графиком линейной функции является прямая.
На этом уроке мы рассмотрим функции:
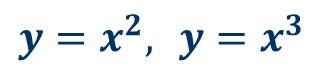
А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.
Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.

Таким образом, зависимость площади квадрата от его стороны является примером функции.
Давайте построим график этой функции.
Составим таблицу значений x, y.
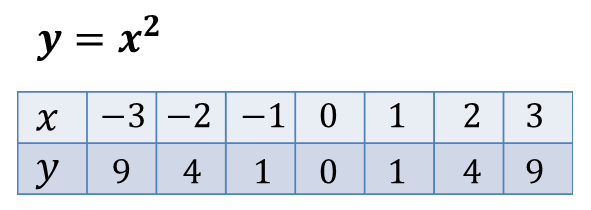
Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.
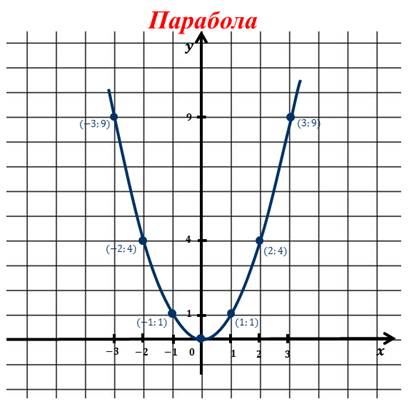
Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек.
Теперь выясним некоторые свойства функции y = x2.
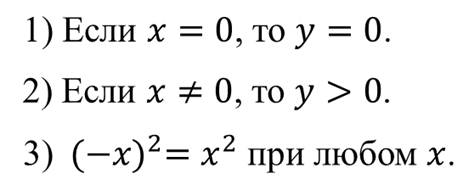
Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.
Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.
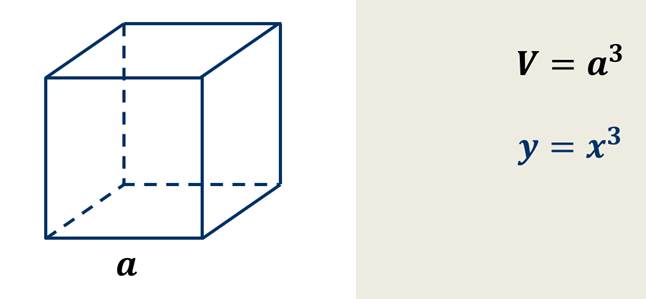
Если мы будем менять длину ребра, то и его объём будет меняться.
Зависимость объёма куба от длины его ребра является примером функции.
Построим график этой функции. Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.

Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.
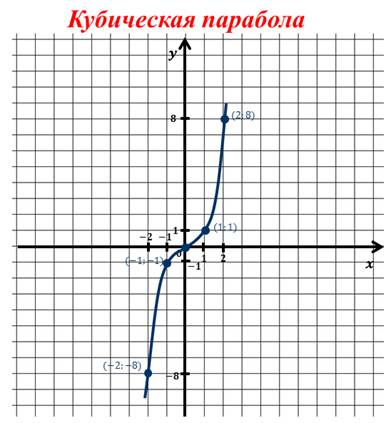
Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз.
Поговорим о свойствах функции игрек равняется икс в кубе.
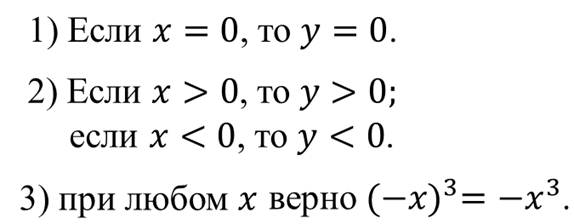
Следовательно, точки графика, которые имеют противоположные абсциссы, расположены симметрично относительно начала координат.
В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.
Также параболу часто можно встретить в архитектуре.



 Получите свидетельство
Получите свидетельство Вход
Вход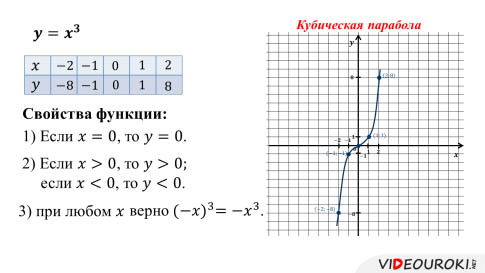



 0
0 41173
41173

