Матрицы

Вопросы:

·     Что такое матрицы?

·     Реализация матриц в языке Python.

·     Операции обработки матриц.

Часто в программировании бывает полезным использование прямоугольных таблиц. Пример такой таблицы – таблица Пифагора или таблица для игры в крестики-нолики. Очевидно, ячейку такой таблицы можно идентифицировать по номерам её строки и столбца. Такие таблицы называются матрицами. Матрица – это прямоугольная таблица, состоящая из элементов одного типа. Каждый элемент матрицы имеет два индекса: номер строки и номер столбца. Обычно при программировании матрицы реализуются через двухмерные массивы. Но так как в языке Python нет массивов, то при реализации матриц к нам на помощь снова приходят списки. Однако мы знаем, что у каждого элемента списка всего один индекс, а у каждого элемента матрицы их должно быть два. Это можно исправить, если в качестве элементов списка будут выступать другие списки. Таким образом, внешний список будет хранить строки матрицы, а внутренние списки – элементы этих строк.

Рассмотрим наиболее распространённые операции над матрицами. Самый простой способ задать матрицу – это в квадратных скобках, обозначающих внешний список, перечислить значения его элементов, то есть внутренние списки. Таким образом, в других, внутренних квадратных скобках мы будем задавать значения элементов внутренних списков.

a = [[1, 2, 3],

     [4, 5, 6],

     [7, 8, 9]]

Эту же запись можно сделать и в одну строку. На несколько строк она была разделена лишь для наглядности.

Попробуем вывести на экран заданную матрицу. Сначала попробуем вывести её как одну переменную, задав в качестве аргумента функции print. Так вся матрица выводится в одну строку, причём вместе с квадратными скобками. Используем другой способ. Для этого создадим новый модуль. Назовём его Matix и сохраним в корневом каталоге интерпретатора, которым мы пользуемся. В этом модуле опишем функцию, которую назовём PrintMatrix. Аргументом этой функции будет список списков. Назовём его a. В теле функции запишем цикл для перебора индексов элементов внешнего списка. Это будет цикл с параметром i, изменяющимся от 0 до длины списка a, не включая последнюю. Внутри этого цикла запишем ещё один цикл для перебора индексов элементов внутреннего списка. Это будет цикл с параметром j, который изменяется от нуля до длины списка a[i], не включая последнюю. Параметр j будет принимать значения индексов элементов этого списка. Внутри этого цикла запишем инструкцию print. Она будет выводить элемент с индексом j строки матрицы a с индексом i. Чтобы сформировать ровные столбцы элементов матрицы, будем для вывода каждого из них выделять по четыре знаковые позиции. Выводить элементы одной строки будем без перехода на следующую строку. После внутреннего цикла в теле внешнего запишем пустую инструкцию print. Она будет выводить на экран символ перехода на следующую строку, чтобы разделить строки матрицы между собой.

def PrintMatrix (a):

    for i in range (len (a)):

        for j in range (len (a[i])):

            print ('{:4d}'.format (a[i][j]))

        print ()

Сохраним описанный модуль, но не будем запускать его на выполнение. Для того, чтобы протестировать описанную функцию, загрузим её из описанного модуля. В интерактивном режиме среды разработки функции можно загружать из модулей, которые находятся в корневом каталоге интерпретатора. Загрузив функцию, вызовем её для вывода заданной матрицы a. Как видим, при таком выводе матрица поделена на строки и столбцы.

Однако, код описанной функции вывода можно сократить. Для этого во внешнем цикле, в параметре row, будем перебирать элементы внешнего списка, а не их индексы, а во внутреннем цикле, в параметре «Икс», будем перебирать элементы списка «Роу». Тогда в инструкции print заменим элемент матрицы a[i][j] на значение параметра x.

def PrintMatrix (a):

    for row in a:

        for x in row:

            print ('{:4d}'.format (x))

        print ()

Сохраним модуль и снова загрузим из него описанную функцию. Вызовем загруженную функцию для матрицы. Как видим, результат совпадает с изначальным.

Как же можно создать новую матрицу, заполненную некоторыми значениями, например, нулями? Кому-то придёт в голову мысль о том, чтобы сначала создать список из одного элемента, после чего с помощью умножения этого списка на количество столбцов матрицы создать его строку. А затем с помощью умножения на количество строк матрицы получить необходимое количество таких строк в списке.

a = [0] * 3

a = [a] * 3

Теперь попробуем изменить значение одного из элементов матрицы. Для этого обратимся к нему по его индексам, и выведем на экран изменённую матрицу.

a[0][1] = 0

PrintMatrix (a)

0 1 0

0 1 0

0 1 0

Оказывается, в ней изменился не только указанный элемент, но и весь столбец. Почему так случилось? Вспомним о том, что мы узнали ранее о копировании списков. Если попытаться передать имя списка в любую инструкцию, то в неё будет передана не копия исходного списка, а ссылка на область памяти, в которой хранится исходный список. То есть при выполнении второго оператора мы заполнили внешний список не копиями внутреннего, а лишь ссылками на область памяти, в которой он хранится, и при обращении к любой строке внешнего списка мы изменяем именно эту область оперативной памяти.

Для того, чтобы создать полноценный список списков, создадим сперва пустой список, после чего запишем цикл, который будет повторяться столько раз, сколько строк должно быть в матрице. В этом цикле будем в конец созданного списка добавлять список, состоящий из элементов, равных нулю, в количестве, равном количеству столбцов матрицы.

a = []

for i in range (3):

    a = a + [[0] * 3]

Снова попробуем изменить один из элементов матрицы и просмотреть её. На этот раз изменился только тот элемент, который мы указали. Также такую матрицу можно создать с помощью выражения-генератора, в котором в качестве элементов создаваемого списка укажем списки, созданные с помощью повторения одного элемента, равного нулю. Попробуем изменить один из элементов созданной матрицы и просмотрим её. Действительно, изменился лишь указанный элемент.

Рассмотрим несколько алгоритмов обработки матриц. В созданный модуль «Матрикс» добавим функцию расчёта суммы элементов матрицы. Назовём её sumMatrix. У неё будет один параметр – матрица, сумму элементов которой нужно вычислить. В теле функции объявим переменную s = 0, в которой будем вычислять сумму элементов матрицы. Теперь для перебора элементов матрицы мы можем воспользоваться вложенным циклом. Просто скопируем такой цикл из функции PrintMatrix, которую мы описали ранее. В цикле же будем увеличивать s на значение параметра x.

def SumMatrix (a):

    s = 0

    for row in a:

        for x in row:

            s = s + x

    return s

Сохраним модуль и в интерактивном режиме среды разработки подключим функцию SumMatrix. Создадим матрицу из 2 строк и 4 столбцов, заполненную тройками. Теперь применим для этой матрицы описанную функцию SumMatrix. В этой матрице каждый элемент равен трём, и всего в ней две строки и четыре столбца. Значит сумма элементов матрицы равна 24. Функция вернула именно это значение. Она работает правильно, но её код можно сократить. Мы можем убрать внутренний цикл, а на его месте записать инструкцию, увеличивающую s на значение функции sum (row). Таким образом, для вычисления суммы элементов строки матрицы мы будем использовать стандартную функцию вычисления суммы элементов списка, уже определённую в языке Python.

def SumMatrix (a):

    s = 0

    for row in a:

        s = s + sum (row)

    return s

Сохраним модуль. Снова подключим из него тестируемую функцию и используем её для вычисления суммы элементов той же матрицы. Результат не изменился. Функция работает правильно.

Рассмотрим несколько определений. Квадратной матрицей называется матрица, в которой количество строк равно количеству столбцов. Элементы квадратной матрицы, у которых номер строки равен номеру столбца, называются её главной диагональю. Противоположная главной диагонали линия элементов называется побочной диагональю. В ней номер строки элемента равен разности размерности матрицы, уменьшенной на единицу, и номера столбца элемента.

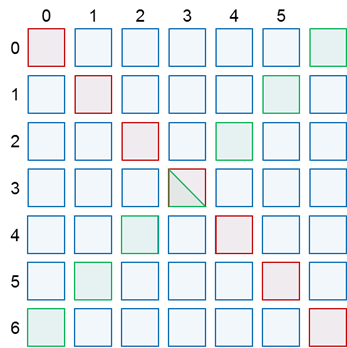
Есть целый ряд задач, связанных с этими определениями. Рассмотрим пример. Очевидно, что главная и побочная диагонали квадратной матрицы делят её на сектора. Создать квадратную матрицу размерностью n строк на n столбцов, заполненную нулями, и заполнить в ней верхний сектор единицами, левый – двойками, правый – тройками и нижний – четвёрками.

Рассмотрим, как делит матрицу главная диагональ. Она делит матрицу на 3 части. Элементы, которые находятся на диагонали, нас не интересуют. В элементах, которые выше главной диагонали, то есть в верхнем и правом секторах, номер строки меньше номера столбца, в элементах ниже её, то есть в левом и нижнем секторах, наоборот, номер строки больше номера столбца. Также матрицу делит побочная диагональ. В элементах, которые выше побочной диагонали, номер строки всегда меньше, чем разность размерности матрицы, уменьшенной на единицу, и номера столбца. Ниже побочной диагонали, наоборот, номер строки больше разности размерности матрицы, уменьшенной на единицу, и номера столбца. Зная, что верхний сектор квадратной матрицы находится выше и главной, и побочной диагоналей, мы можем соединить два соответствующих условия союзом И, получив таким образом условие принадлежности элемента матрицы к верхнему сектору. Аналогично выводятся условия принадлежности элемента матрицы и к остальным секторам.

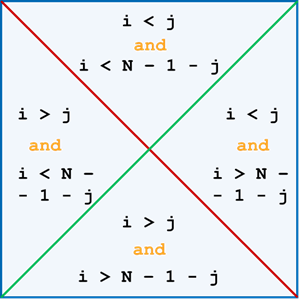
Напишем программу для решения задачи. Организуем ввод размерности матрицы. Для этого запишем бесконечный цикл, а в нём – инструкцию для вывода на экран запроса на ввод n без перехода на следующую строку. Дальше запишем инструкцию для считывания значения n. Запишем выражение–генератор для создания матрицы a из n строк и n столбцов, заполненной нулями.

Теперь будем перебирать элементы матрицы и проверять, к какому сектору они принадлежат. Так как мы будем анализировать индексы элементов матрицы, то в циклах будем перебирать именно индексы, а не сами элементы. Номер строки будет в параметре i, а номер столбца – в j. В цикле запишем ветвление с условием принадлежности текущего элемента списка к верхнему сектору, то есть то, что i < j and i < n – 1 - j. Если это условие выполняется, присвоим текущему элементу матрицы значение 1. Если элемент списка не принадлежит к верхнему сектору – проверим его принадлежность к левому сектору. Если он принадлежит к левому сектору – присвоим ему значение 2. Точно так же будем проверять принадлежность элементов к правому и нижнему секторам. И в случае принадлежности к одному из них будем присваивать элементу соответствующее значение. После цикла выведем элементы матрицы на экран. Для этого загрузим из описанного ранее модуля Matrix функцию PrintMatrix и вызовем её для матрицы a.

print ('n =')

n = int (input ())

a = []

for i in range (n):

    a = a + [[0] * n]

for i in range (n):

    for j in range (n):

        if i < j and i < n - 1 - j:

            a[i] = 1

        elif i < j and i > n - 1 - j:

            a[i] = 2

        elif i > j and i > n - 1 - j:

            a[i] = 3

        elif i > j and i < n - 1 - j:

            a[i] = 4

from Matrix import PrintMatrix

PrintMatrix (a)

Сохраним описанный модуль в одном каталоге с модулем Matrix и запустим его на выполнение. Введём размерность, равную 10. Матрица с пронумерованными секторами была выведена на экран. Программа работает правильно. Задача решена.

Для работы с многомерными массивами и проведения сложных математических расчётов есть расширение для языка Python, которое называется NumPy. Его вы можете рассмотреть самостоятельно, если захотите.

Мы узнали:

·     Матрицей называется прямоугольная таблица из элементов одного типа. Каждый элемент матрицы имеет 2 индекса – номер строки и номер столбца матрицы, в которых он располагается.

·     Для реализации матриц в языке Python используются списки, элементами которых являются списки.