Силы всемирного тяготения. Закон всемирного тяготения

Вы уже знакомы с явлением всемирного тяготения из курса девятого класса. Так же мы говорили о том, что все тела, обладающие массой, притягиваются друг к другу. Из второго закона Ньютона следует, что любая равнодействующая сила равна произведению массы тела и ускорения, сообщаемого этой силой: .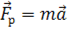

Так, например, сила тяжести равна произведению массы тела и ускорения свободного падения: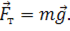

Но, как мы уже выяснили, ускорение свободного падения не зависит от массы тела, из чего можно сделать вывод, что гравитационные силы сообщают ускорение, которое не зависит от массы тела!

Это поразительное свойство можно объяснить только тем, что гравитационные силы пропорциональны массе тела, на которое они действуют. А теперь, вспомним третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю, направленными по одной прямой в противоположных направлениях: .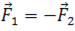

В частности, если Земля действует на Луну с некоторой силой, то и Луна должна действовать на Землю с этой силой. Значит, гравитационная сила, возникающая между двумя телами пропорциональна массам обоих тел.

Рассмотрим теперь ускорение, с которым двигается Луна. Напомним, что любое криволинейное движение является ускоренным. Движение Луны вокруг Земли хорошо известно людям: период обращения Луны вокруг Земли составляет примерно 27,3 земных суток, а средний радиус орбиты Луны составляет 384 тыс. километров. Исходя из этого, мы можем подсчитать центростремительное ускорение Луны:

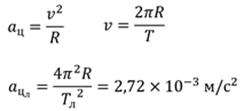
Если мы сравним теперь получившуюся величину с ускорением свободного падения на Земле, то убедимся, что ускорение Луны примерно в 3600 раз меньше, чем ускорение свободного падения на Земле:

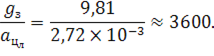
А теперь, сравним радиус Земли с расстоянием между Землёй и Луной:

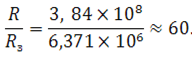
 Оказывается, что радиус Земли примерно в 60 раз меньше, чем расстояние между Землей и Луной. Заметим, что 60² — это 3600. Из этого можно заключить, что сила тяготения между двумя телами уменьшается пропорционально квадрату расстояния между этими телами.

Исходя из всего вышеперечисленного, формулировка закона всемирного тяготения такова: сила взаимного притяжения двух тел прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними.

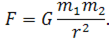
Необходимо отметить, что если тела не являются материальными точками, то за расстояние между ними принимается расстояние между центрами тяжести этих тел. В формуле мы видим коэффициент пропорциональности, который называется гравитационной постоянной. Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массами 1 кг, если расстояние между ними составляет 1 метр.

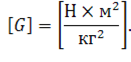
Гравитационная постоянная является очень важной константой, поскольку именно с её помощью люди смогли вычислить массу Земли, Луны, Солнца и так далее. Но как вычислить саму гравитационную постоянную?

Впервые гравитационная постоянная была измерена Генри Кавендишем в 1798 году. С помощью крутильных весов, ему удалось определить значение гравитационной постоянной достаточно точно (оно почти совпадает с принятым сегодня значением).

Крутильные весы представляют собой следующую установку: на тонкой упругой нити подвешено лёгкое коромысло с двумя шарами на концах. Рядом закреплены два значительно более тяжёлых шара (в эксперименте Кавендиша легкие шары имели массу 775 г, а тяжёлые – 49,5 кг). В результате гравитационного взаимодействия, коромысло поворачивалось и закручивало нить. Зная упругие свойства нити, Кавендишу удалось измерить силу притяжения. Поскольку, массы шаров ему были известны, так же, как и расстояние между ними, Кавендиш смог вычислить гравитационную постоянную.

Необходимо отметить, что закон всемирного тяготения дает точный результат, в трех случаях:

1)               Если оба тела имеют форму шара и являются однородными.

2)               Если размеры тел ничтожно малы, по сравнению с расстоянием между ними.

3)               Если одно из тел обладает формой шара и его размеры многократно больше размеров второго тела любой формы.

Примеры решения задач.

Задача 1. Юпитер обладает массой 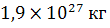и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.

Поскольку закон всемирного тяготения является одним из универсальных законов природы, он одинаково выполняется для всех тел, имеющих массу. Рассмотрим произвольное тело (масса и размеры которого ничтожно малы по сравнению с массой и размерами Юпитера).

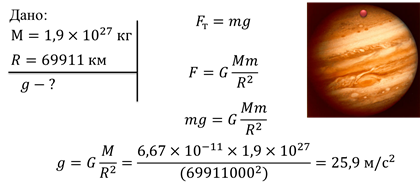
Задача 2. Вычислите, на какой высоте над поверхностью Земли должен находиться геостационарный спутник.

На первый взгляд может показаться, что в задаче нет исходных данных. Но если мы внимательно рассмотрим ситуацию, то убедимся, что некоторые данные у нас есть. В первую очередь, — это период обращения спутника: разумеется, он должен быть равен периоду обращения Земли вокруг своей оси. И самое главное: спутник должен двигаться с постоянной скоростью, поскольку Земля тоже двигается с постоянной скоростью.

Необходимо отметить, что в задачах мы принимали орбиты планет за окружности для упрощения расчетов. В действительности, планеты Солнечной системы двигаются по эллиптическим орбитам, поэтому, когда мы говорим о расстоянии от планеты до Солнца, мы имеем ввиду средний радиус её орбиты.