Проецирование предмета на плоскости проекций даёт нам представление о форме самого предмета только с одной стороны. И, чтобы получить представление о форме предмета в целом, нужно проанализировать и сравнить между собой отдельные его проекции (например, фронтальную, горизонтальную и профильную).
Но оказывается, предмет можно спроецировать на плоскость проекций таким образом, чтобы на созданном изображении было видно сразу несколько его сторон. Полученное таким образом изображение называется наглядным.

Его используют для реализации технического замысла автора при выполнении проектирования и конструирования разных объектов.
Давайте посмотрим на четыре изображения куба. Что вы можете сказать о первых двух? Правильно, первые два — это перспективные изображения. Причём первое — с одно точкой схода, а второе — с двумя.

Два других изображения называются аксонометрическими проекциями куба. Причём, вот эта проекция называется диметрической, а эта — изометрической.
А какое изображение из четырёх наиболее чётко передаёт размеры рёбер куба? Действительно, два последних А какое именно из этих изображений более точно отражает их величину? Конечно последнее. Ведь на нём все рёбра и грани одинаковой величины.
Таким образом, два первых изображения дают нам представление о геометрической форме предмета. А вот аксонометрические проекции (третье и четвёртое изображения) дают представление и о форме, и о соотношении размеров рёбер и сторон куба.
Термин «аксонометрия» происходит от двух греческих слов: «аксон» — ось и «метрео» — измеряю, считаю. То есть построение аксонометрических изображений детали или другого предмета связано с измерением и построением размеров по осям прямоугольных координат.
Таким образом, аксонометрическая проекция — это изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на какую-нибудь плоскость. Эта плоскость называется картинной плоскостью аксонометрических проекций. А проекции координатных осей называются аксонометрическими осями.

В зависимости от расположения осей прямоугольных координат X, Y, Z относительно плоскости аксонометрических проекций и направления проецирующих лучей получают прямоугольную и косоугольную проекции.
К прямоугольным аксонометрическим проекциям относятся изометрическая, диметрическая и триметрическая проекции.

Кратко диметрическую проекцию называют диметрией (то есть двойное измерение), изометрическую — изометрией (равное измерение по осям), а триметрическую — триметрией (измерение по всем трём осям различно)
К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям.
Коэффициент искажения (k) — это отношение размера аксонометрической проекции отрезка, имеющего направление какой-либо оси координат, к его действительному размеру. Например, при действительном размере 100 мм и показателе искажения 0,82 размер аксонометрической проекции равен 100 × 0,82 = 82 мм.
Вообще же, коэффициенты искажения различны в изометрических и диметрических аксонометрических проекциях. Однако для упрощения вычисления показателей искажения ГОСТ 3453-59 рекомендует строить изометрическую проекцию без сокращения по аксонометрическим осям.

А диметрическую проекцию без сокращения по аксонометрическим осям X, Z. И с сокращением 0,5 по аксонометрической оси Y. В этом случае изображение получается несколько увеличенным, но наглядность его не ухудшается.
Существуют три правила построения аксонометрических проекций. Их надо запомнить.
Итак, правило первое: длина откладывается по оси х, высота — по оси z, а ширина — по оси у.
Второе правило: все измерения выполняются только по аксонометрическим осям или прямым, параллельным им.

И третье правило: все прямые линии, параллельные друг другу или осям координат (x, y, z), на комплексном чертеже в аксонометрических проекциях остаются параллельными между собой и соответствующим аксонометрическим осям.

Наиболее распространёнными являются прямоугольная изометрическая (прямоугольная изометрия) и косоугольная фронтальная диметрическая (фронтальная диметрия) проекции, в которых объект изображается в трёх проекциях так, чтобы можно было хорошо увидеть его форму с трёх сторон. Но прежде, чем приступать к построению этих проекций, необходимо научиться строить их оси координат.
Для начала рассмотрим последовательность построения осей диметрической проекции.
Итак, шаг первый. Построение и обозначение осей X и Z. Здесь всё просто. Берём угольник и строим две оси, расположенные под прямым углом друг к другу. Точка их пересечения (точка О) — это начало координат.
Шаг второй. Построение оси Y. Итак, чтобы построить ось Y из точки О нужно провести биссектрису прямого угла XОZ, то есть построить угол в 45°. Для этого можно воспользоваться транспортиром.
Можно использовать угольник, с углами 90°, 45°, 45° и линейку.
А если их нет, то поможет циркуль. Для этого из вершины угла О произвольным радиусом проведём дугу до пересечения со сторонами угла XOZ. Получим две точки, например, n и k.
Из полученных точек проведём дуги радиусом R, несколько большим половины длины дуги nk, до взаимного пересечения в точке m.
Вершину угла О соединим с точкой m прямой, которая разделит наш угол XOZ на две равные части и продолжим её за точку О. Вот мы и построили искомую ось Y.

Шаг третий. Обозначение коэффициентов искажения по осям. Здесь помним, что, в диметрической проекции по осям X и Z и по параллельным им прямым откладывают натуральные размеры. А вот по оси Y и прямым, параллельным ей, — размеры, уменьшенные в два раза.
Теперь давайте с вами построим наглядное изображение прямоугольного параллелепипеда в диметрической проекции.
Итак, шаг первый. Построение осей диметрии и нижнего основания прямоугольного параллелепипеда.
Построение изображения детали в аксонометрических проекциях всегда начинаем с её нижнего основания. А по какой оси мы откладываем размер длины детали? Правильно, по оси X.
По какой оси откладывается размер ширины детали? Всё верно — Y. При этом не забываем, что в диметрии ширина детали уменьшается в два раза
А как расположены стороны основания параллелепипеда?.. Действительно, они параллельны осям X и Y и попарно равны.
Первый этап построения предмета в диметрии — всегда построение его основания.

Шаг второй. Построение проекции вертикальных рёбер.
Для построения вертикальных рёбер мы с вами должны из вершин основания провести прямые, параллельные вертикальной оси z.
Затем, на этих прямых и на оси z мы откладываем значение высоты детали (для этого можно воспользоваться, например, циркулем).
Шаг третий. Построение проекций верхнего основания и боковых граней.
Достаточно лёгкий шаг: достаточно соединить полученные в прошлом шаге точки прямыми линиями.
И последний, четвёртый шаг заключается в определение видимости граней и обводке чертежа.
Следующая наша задача — научиться построению осей прямоугольной изометрической проекции. Для этого:
Проведём вертикально ось Z и выберем на ней произвольную точку О, которая станет нашим началом координат.
Затем можно поступить несколькими способами. Первый, и самый простой из них, — это воспользоваться транспортиром для того, чтобы отложить от оси Z два угла по 120°.
Можно воспользоваться угольником на 45° и линейкой. Для этого мы должны поставить угольник на линейку и подвести их оси Z так, чтобы короткий катет угольника совпал с ней. Затем, придерживая линейку рукой, отводим угольник в сторону так, чтобы гипотенуза угольника проходила через начало оси Z. И проводим нашу ось Х.
Теперь переворачиваем угольник, не меняя положения линейки, и повторяем те же операции для построения оси Y.
Третий способ построения осей предполагает использование циркуля.
Итак, выберем на вертикально расположенной оси Z произвольную точку — точку О. Из этой точки произвольным радиусом проведём дугу. Точку пересечение дуги с продолжением оси Z обозначим, например, через А.

Теперь из этой точки как из центра проведём дугу тем же радиусом АО до взаимного пересечения двух дуг в точках В и С.
Соединив точку О с точками В и С получим оси X и Y изометрической проекции.
Так как оси X, Y, Z наклонены к фронтальной плоскости под одинаковыми углами, то их проекции изображаются меньше их натуральной величины — 0,82 от натуральной величины.
Но, как мы уже упоминали, для упрощения вычисления показателей искажения ГОСТ 3453-59 рекомендует строить изометрическую проекцию без сокращения по аксонометрическим осям, то есть в натуральную величину 1 : 1 : 1. В этом случае наглядное изображение объекта увеличивается в 1,22 раза.
Теперь давайте с вами построим наглядное изображение уже знакомого нам прямоугольного параллелепипеда в изометрической проекции.
Итак, шаг первый. Построение осей изометрии и нижнего основания прямоугольного параллелепипеда.
Как и в случае с диметрией, построение изображения детали начинаем с её нижнего основания. При этом не забываем, что в изометрии размеры детали не изменяются.
Шаг второй. Построение проекции вертикальных рёбер.
Для построения вертикальных рёбер мы с вами должны из вершин основания провести прямые, параллельные вертикальной z.
Затем, на этих прямых и на оси z мы откладываем значение высоты детали.
Шаг третий. Построение проекций верхнего основания и боковых граней.

И последний, четвёртый шаг — определение видимости граней и обводка чертежа.
Обратите внимание: при построении аксонометрических проекций предметов, имеющих форму четырёхугольных прямых призм, из каждой вершины всегда выходят три луча (видимые или невидимые), направленные параллельно осям аксонометрии.

 Получите свидетельство
Получите свидетельство Вход
Вход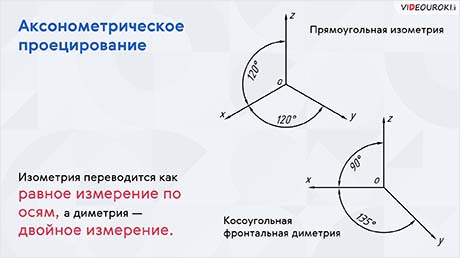




 1570
1570