Простые механизмы. Коэффициент полезного действия простых механизмов

На одном из прошлых уроков мы с вами говорили о механической работе — физической величине, которая характеризует процесс перемещения тела под действием силы. Для облегчения совершения механической работы издавна используются различные приспособления — простые механизмы.

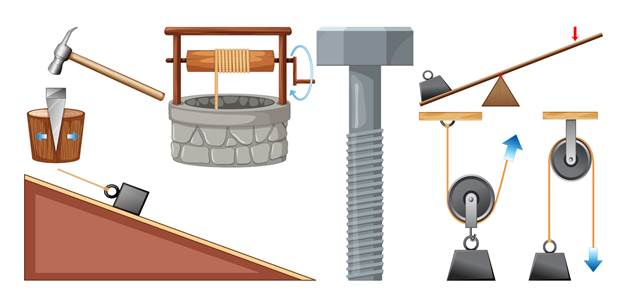
Простые механизмы — это устройства, в которых работа совершается только за счёт механической энергии.

Нас окружают устройства, работающие за счёт электроэнергии, за счёт энергии сгорания топлива и так далее. Но так было не всегда. В давние времена практически всю работу выполняли руками или с помощью животных, за счёт ветра или течения воды, то есть за счёт механической энергии. А помогали в этом простые механизмы.

К простым механизмам относятся: рычаг и его разновидности — блок и ворот; наклонная плоскость и её разновидности — клин и винт.

В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить силу, действующую на тело, в несколько раз. Ведь наши мускульные силы ограничены. Мы, например, не можем за один раз поднять и перенести с одного места на другое поддон кирпичей. Зато мы можем потратить больше времени, пройти большее расстояние туда-сюда и перенести кирпичи по несколько штук за один подход.

Таким образом, простые механизмы служат для преобразования силы. Их применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.

Одним из наиболее распространённых простых механизмов является рычаг. Именно он позволяет малой силой уравновесить большую. Итак, рычагом является любое твёрдое тело, которое может поворачиваться относительно неподвижной оси или опоры под действием сил. Различают рычаги первого и второго рода.

Рычагом первого рода называют рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Это коромысло равноплечих весов, железнодорожный шлагбаум, ножницы и так далее.

Рычаг второго рода — это рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу. Это гаечные ключи, щипцы для раскалывания орехов, двери и прочее.

А теперь давайте проведём такой опыт. Возьмём небольшую доску длиной один метр и поместим её на неподвижную опору ровно посередине. На расстоянии в 0,25 м от опоры поставим гирю весом 14 Н.

Надавим на свободный конец рычага динамометром и поднимем гирю, установив рычаг горизонтально. Странно, динамометр у нас показывает силу примерно в 7 Н. Почему же неравные силы, приложенные к рычагу, удерживают его в равновесии? Правильно, потому, что результат действия силы на рычаг определяется не только её модулем, но и длиной плеча.

Давайте вспомним, что плечом силы называется кратчайшее расстояние от точки опоры до линии действия этой силы. Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и будет плечом данной силы.

Изобразим схему проведённого опыта. Итак, кроме сил F₁ и F₂, плечи которых равны соответственно l₁ и l₂, на рычаг действуют ещё две: сила тяжести рычага и сила упругости опоры. Однако, как мы видим, плечи этих сил равны нулю. Поэтому они на равновесие рычага не влияют.

А теперь давайте сравним силы F₁ и F₂ и их плечи:

Нетрудно заметить, что сила F₂ в два раза меньше силы F₁. Но вот её плечо в два раза больше. Если бы мы смогли увеличить плечо силы F₂ в два, три или десять раз, то модуль этой силы уменьшился бы во столько же раз. Но самое интересное в том, что для данного рычага произведение модуля силы на её плечо осталось бы неизменным:

Это произведение называется моментом силы (иногда его называют ещё вращающим или крутящим моментом):

Единица измерения — ньютон, умноженный на метр:

Мы не зря в формуле поставили знак «плюс-минус». Дело в том, что принято считать: если сила стремится повернуть рычаг по ходу часовой стрелки, то момент этой силы положительный, а если против — отрицательный.

А теперь давайте рассчитаем момент силы F₁:

Как видим, момент этой силы равен моменту силы F₂. Из этого мы с вами можем сделать важный вывод: рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки:

Все сделанные выводы справедливы и для рычага второго рода.

А возможно ли равновесие рычага, когда на него действуют несколько (больше двух) сил? Конечно, возможно. Но для этого необходимо, чтобы алгебраическая сумма моментов всех сил, вращающих рычаг как по ходу часовой стрелки, так и против него, была равна нулю:

Ещё одним простым механизмом, служащим для поднятия грузов, является блок. Блок — колесо с жёлобом, укреплённое в обойме. По жёлобу блока пропускают верёвку, трос или цепь.

Принято различать два вида блоков — подвижный и неподвижный.

Неподвижным блоком называют такой блок, ось которого закреплена и при подъёме грузов не поднимается и не опускается.

Неподвижный блок можно рассматривать как равноплечий рычаг первого рода, у которого плечи сил равны радиусу колеса. Тогда из условия равновесия рычага следует, что неподвижный блок не даёт выигрыша в силе. Однако он изменяет её направление.

Встаёт вопрос: зачем применять неподвижный блок, если выигрыша в силе нет? Ведь в этом случае для подъёма груза можно было бы использовать любую перекладину.

Можно, но проигрышно, так как придётся преодолевать силу трения скольжения верёвки по перекладине, которая значительно больше силы трения качения в подшипнике блока.

Теперь рассмотрим подвижный блок, то есть блок, ось которого поднимается и опускается вместе с грузом.

Итак, подвесим к блоку груз весом 6 Н. Один конец перекинутой через блок нити закрепим, а за другой будем равномерно поднимать груз. Динамометр показывает, что прилагаемая к концу верёвки сила равна примерно 3 Н, то есть в два раза меньше веса груза. Значит, подвижный блок даёт выигрыш в силе в два раза. Вспомним, как это объясняется.

Итак, для удобства будем считать, что блок у нас идеальный — невесом и в нём отсутствуют силы трения. Тогда на блок будут действовать: вес груза и силы упругости нити (причём сила Т₂ равна по модулю силе, поднимающей груз).

При движении груза наш блок поворачивается относительно мгновенной оси О. Значит подвижный бок можно рассматривать, как рычаг второго рода и к нему можно применить правило моментов.

Из рисунка видно, что плечо силы Р равно радиусу блока, а плечо силы F — его диаметру:

Тогда из правила моментов следует, что сила, прикладываемая для подъёма груза, в два раза меньше веса этого груза:

Значит, подвижный блок даёт выигрыш в силе в два раза.

Мы видим, что с помощью простых механизмов можно получить выигрыш в силе. Но дают ли простые механизмы выигрыш в работе?

Давайте рассчитаем работу, которую совершает сила при равномерном подъёме груза на высоту h с помощью гладкой наклонной плоскости длиной l.

Итак, на груз действуют три силы: сила тяги, направленная вдоль плоскости, сила тяжести и сила нормальной реакции опоры.

Запишем основное уравнение динамики в общем виде:

Направим ось Ox вдоль наклонной плоскости в сторону перемещения груза и спроецируем второй закон Ньютона на эту ось:

Из полученного равенства выразим силу F и при этом учтём, что синус угла наклона плоскости равен отношению высоты плоскости к её длине:

То есть для равномерного поднятия груза с помощью наклонной плоскости необходимо приложить силу, во столько раз меньшую силы тяжести груза, во сколько раз длина наклонной плоскости больше её высоты.

Теперь вспомним, что работа равна произведению модуля силы на модуль перемещения и на косинус угла между направлением вектора силы и вектора перемещения (в нашем случае последний множитель равен единице, так как направления векторов силы и перемещения совпадают):

Подставим в записанное равенство выражение для силы тяги, найденное нами ранее:

После упрощения получим, что работа приложенной к грузу силы F равна работе, которую нужно совершить, чтобы равномерно поднять груз на высоту h, не используя наклонной плоскости.

Аналогично можно показать, что не дают выигрыша в работе ни рычаги, ни блоки.

Ещё древние учёные сформулировали правило («золотое правило механики»), применяемое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии:

При рассмотрении простых механизмов мы не учитываем трение, а также вес самих механизмов. В реальных условиях это необходимо учитывать. Поэтому часть работы совершается силой на перемещение отдельных частей механизма и против силы трения. Работа же по подъёму груза (полезная работа (А_п)) будет меньше полной работы (А), совершённой силой, приложенной к механизму.

Эффективность работы механизма характеризуют коэффициентом полезного действия (КПД механизма).

Коэффициент полезного действия — это физическая величина, равная отношению полезной работы ко всей затраченной работе:

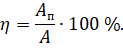
Так как полезная работа всегда (подчёркиваем, всегда) меньше совершённой, то КПД механизма всегда меньше 100 %.

Чтобы увеличить КПД, необходимо уменьшить трение и массу простого механизма. Тогда уменьшится совершённая работа, приблизившись к полезной работе. А КПД будет стремиться к 100 %.