Определение расстояний и размеров тел в Солнечной системе

Вы уже знаете, что ещё в Древней Греции учёными и мыслителями было установлено, что наша планета не является плоской, а имеет шарообразную форму. Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений древнего мира.

Первый известный науке метод определения размеров Земли применил греческий учёный Эратосфен, живший в Египте. Его идея была достаточно проста. Итак, Эратосфен выбрал два города — Александрию и Сиену (ныне Асуан) — расположенных на одном земном меридиане.

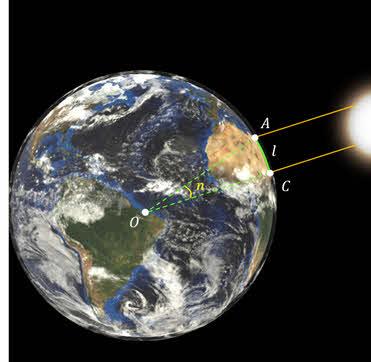
Далее он обозначил длину дуги меридиана между двумя городами через l, а её угловое значение в градусах как п.

Тогда длина дуги в 1^о выбранного меридиана равна

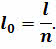
А длина всей окружности меридиана: L = 360^o ∙ l₀.

С другой стороны, он знал, что длина окружности равна: L = 2πR.

Приравняв правые части последних двух уравнений, легко получить искомый радиус земного шара:

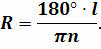
Теперь было необходимо определить длину дуги меридиана в градусной мере. Очевидно, что она равна разности географических широт Александрии и Сиены. Так вот, чтобы определить эту разность Эратосфен придумал хитрый способ. Он знал, что в полдень дня летнего Солнцестояния в Сиене Солнце находится в зените и освещает дно самых глубоких колодцев. А в Александрии Солнце до зенита не доходит. Поэтому шест, вбитый вертикально в землю должен отбрасывать тень. Измерив длину этой тени можно легко определить искомую длину дуги меридиана, которая у Эратосфена оказалась равной 7,2^о.

Ну а расстояние между Александрией и Сиеной ему было хорошо известно: оно составляло пять тысяч греческих стадий.

Подставив все данные в формулу для длины окружности меридиана, Эратосфен получил значение в 250 000 стадий.

Стадий — это весьма неоднозначная единица измерения расстояния. Но, как правило, за стадий принимали расстояние, которое проходит легковооружённый воин за промежуток времени от появления первого луча солнца при его восходе до того момента, когда весь солнечный диск окажется над горизонтом.

Однако если учесть, что расстояние между Александрией и Асуаном по прямой примерно равно 844 километрам, то можно полагать, что одна стадия примерно равна 169 метрам.

Тогда искомая длина всей окружности меридиана равна 42 250 километрам, что совсем не плохо для того времени.

Современная наука располагает более точными способами измерения расстояний на земной поверхности. Одним из них является метод триангуляций, основанный на явлении параллактического смещения.

Параллактическое смещение — это изменение направления на предмет при перемещении наблюдателя. С его помощью можно измерить расстояние на основе измерения длины одной из сторон (базиса) и двух прилегающих к ней углов в треугольнике.

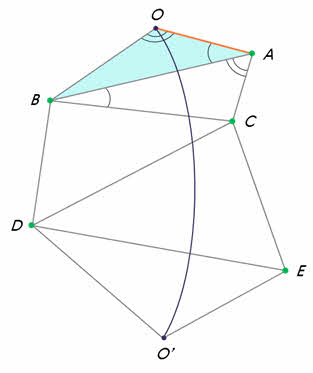
Суть метода триангуляций состоит в следующем. По обе стороны дуги, длину которой нужно измерить, выбирается несколько точек на расстоянии не более 50 километров друг от друга, на которых устанавливаются геодезические вышки. При этом из каждой точки должны быть видны по крайней мере две другие точки. Далее тщательным образом измеряется длина базиса (с точностью до одного миллиметра). После этого с вершины вышки при помощи теодолита измеряются углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон по известным тригонометрическим формулам. Проводя затем измерение углов из пунктов, расстояние между которыми уже вычислено, можно узнать длину очередных двух сторон и так далее. Затем, по вычисленным сторонам, определяется искомая длина дуги.

В XVIII веке использование триангуляционных измерений в экваториальных широтах и вблизи северного полярного круга, показало, что длина дуги в 1^о меридиана не одинакова и увеличивается к полюсам. Из этого следовало, что наша планета не является идеальным шаром и её полярный радиус почти на 21 километр короче экваториального. Поэтому в геодезии и форму Земли считают геоидом, то есть телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.

В настоящее время форму Земли принято характеризовать следующими физическими характеристиками:

·                   полярное сжатие — 0,0033528;

·                   экваториальный радиус — 6378,1 км;

·                   полярный радиус — 6356,8 км;

·                   средний радиус — 6371,0 км;

·                   и длина окружности экватора — 40 075,017 км.

Долгое время загадкой для многих астрономов являлось истинное расстояние от Земли до Солнца. Измерить его смогли лишь во второй половине XVIII века, когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.

Горизонтальным параллаксом называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения.

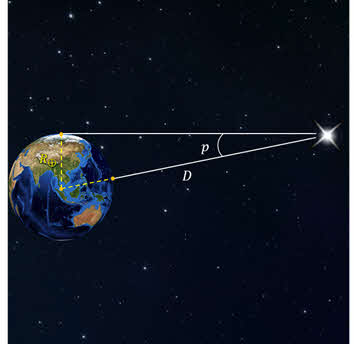
Зная горизонтальный параллакс светила, можно, по известным тригонометрическим соотношениям, определить его расстояние от центра Земли:

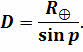
Очевидно, что чем дальше расположено светило, те меньше его горизонтальный параллакс. Например, наибольший параллакс, в среднем 57ʹ, имеет спутник Земли — Луна. У Солнца он значительно меньше и примерно составляет 8,794ʹʹ. Такому параллаксу соответствует среднее расстояние от Земли до Солнца, примерно равное 149,6 миллиона километров.

На одном из прошлых уроков мы говорили о том, что это расстояние в астрономии принимается за одну астрономическую единицу. С её помощью удобно измерять расстояния между телами в Солнечной системе.

Но вернёмся к нашей формуле. Итак, из геометрии вам должно быть известно, что при малых значениях угла его синус примерно равен самому углу, выраженному в радианах. Если учесть, что в одном радиане содержится 206 265ʹʹ, то легко можно получить формулу, удобную для вычислений:

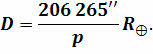
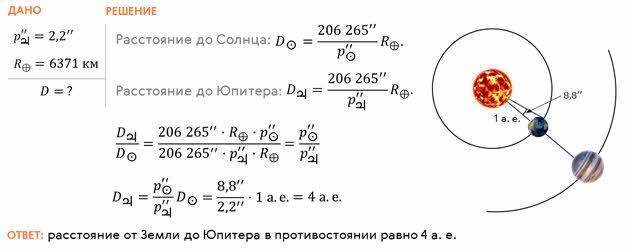
Для примера, давайте с вами определим расстояние от Земли до Юпитера в момент противостояния, если его горизонтальный параллакс был равен 2,2ʹʹ. Радиус Земли примем равным 6371 километру.

Эту же задачу можно было решить несколько иначе.

В настоящее время для более точного определения расстояний до тел в Солнечной системе применяется более точный метод измерений — радиолокационный. Измерив время, необходимое для того, чтобы радиолокационный импульс достиг небесного тела, отразился и вернулся на Землю, вычисляют расстояние до этого тела по формуле:

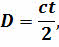
где с — это скорость света в вакууме.

С разработкой методов определения расстояний до тел в Солнечной системе учёным не составило большого труда придумать и способ определения их размеров. В частности, при наблюдениях небесного тела Солнечной системы с Земли можно измерить угол, под которым оно видно наблюдателю, то есть его угловой размер (или угловой диаметр), а, следовательно, и угловой радиус.

А зная угловой радиус и расстояние до светила, можно вычислить его линейный радиус:

.

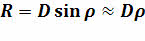Только в этой формуле угловой радиус должен быть выражен в радианах.

Если в записанное уравнение подставить формулу для определения расстояний методом горизонтального параллакса и упростить её, используя тот факт, что значения углов ρ и р малы, то получим формулу, по которой можно определять линейные размеры небесных тел:

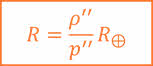
Но помните, пользоваться ей можно тогда, когда видны диски светил.

Для примера давайте решим с вами такую задачу. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус равен 5,5’’, а горизонтальный параллакс — 14,4’’. Чему равен линейный радиус Меркурия?