Исследование зависимости сопротивления проводника

В первой части нашей работы с помощью экспериментальной установки мы будем исследовать зависимость сопротивления проводника от его длины.

Для выполнения этой работы мы будем использовать оборудование из третьего комплекта в составе: источник тока, двухпредельный вольтметр и амперметр, ключ, реостат, соединительные провода и набор проволочных резисторов на подставке.

Прежде чем приступить к работе давайте с вами вспомним, что электрическое сопротивление — это физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока в нём.

При этом, как было экспериментально установлено, сопротивление конкретного проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен:

Именно зависимость сопротивления проводника от его длины мы с вами и должны будем проверять. Однако для выполнения данной работы эта формула нам не подходит. А, судя по предложенному оборудованию, сопротивление проводника мы будем находить на основании закона Ома для участка цепи. Ведь ещё в 1826 году Георг Ом экспериментально установил, что сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению:

Зная величину напряжения на концах проводника и ток в нём, по закону Ома можно вычислить электрическое сопротивление проводника, как отношение напряжения на концах проводника к силе тока в проводнике:

Итак, приступим к выполнению. Для начала давайте взглянем на набор проволочных резисторов и подумаем, какие из них мы будем использовать в данной работе. Как мы недавно вспоминали, электрическое сопротивление проводника зависит от удельного сопротивления проводника, от длины проводника и площади его поперечного сечения. Для установления зависимости сопротивления от длины проводника необходимо выбрать проводники, отличающиеся только длиной и имеющие одинаковые остальные параметры (площадь поперечного сечения и материал). Данному условию удовлетворяют три нихромовых проводника, расположенные в верхней части панели.

С проводниками разобрались, теперь соберём экспериментальную установку. Для этого последовательно с источником тока соединим ключ, амперметр на предел измерения 0,6 А, реостат и набор проволочных резисторов так, чтобы в цепь был включён короткий нихромовый проводник, длина которого примерно равно одной трети длины длинного проводника. А чтобы измерить напряжение на концах исследуемого резистора, параллельно к нему подключим вольтметр, подключённый на предел измерения 3 В.

Далее мы с вами нарисуем электрическую схему нашей установки. При этом, обратите внимание, как таковой схемы для набора проволочных резисторов нет. Поэтому можно поступить двумя способами: либо изобразить обычный резистор, либо попробовать схематически, например, как мы, перерисовать всю панель.

Теперь запишем формулы, которыми будем пользоваться при выполнении данной работы. Во-первых, запишем формулу для определения сопротивления проводника через его геометрические размеры:

Во-вторых, — закон Ома для участка цепи:

А из него находим, что электрическое сопротивление проводника равно отношению напряжения на концах проводника к силе тока в проводнике:

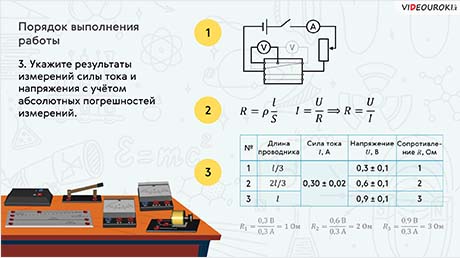
Так как по условию задания нам необходимо провести несколько измерений, то целесообразно оформить их в виде таблицы. В первой колонке мы укажем номера опытов. Во второй — примерную длину проводников (визуально это l/3, l/2, l).

В третью колонку мы занесём значения силы тока с учётом погрешности измерения (они нам даны по условию задачи). Четвёртую колонку мы оставим для значений напряжения на концах проводников. А последнюю колонку отведём для сопротивлений.

Прежде чем приступить непосредственно к работе ещё раз внимательно проверьте вашу электрическую цепь. Проверьте, чтобы в цепь был включён самый короткий проводник. Особое внимание обратите на соблюдение полярности подключения обоих приборов.

Если всё в порядке, то включаем источник питания и замыкаем ключ. Далее, с помощью реостата устанавливаем в цепи заданную нам по условию силу тока. При этом не забываем, что на прибор мы должны смотреть перпендикулярно шкале прибора.

Установив требуемое значение силы тока, снимаем показания с вольтметра. Итак, у нас напряжение на концах резистора оказалось равным примерно 0,3 В. Размыкаем ключ и заносим значение напряжения в таблицу, с учётом погрешности измерений:

Теперь включим в цепь вторую часть провода и параллельно ему — вольтметр. Замкнём ключ. Вольтметр показывает нам примерно 0,6 В. Опять размыкаем ключ и заносим значение напряжения в таблицу.

И, наконец, включаем в цепь проводник на всю его длину.

Напряжение на концах проводника оказывается равным примерно 0,9 В.

Закончив с прямыми измерениями, приступаем к нахождению сопротивления для каждого из трёх случаев. Для чего в расчётную формулу поочерёдно подставляем наши значения силы тока и напряжения.

Теперь нам хорошо видно, что при увеличении длины проводника увеличивается и его сопротивление, причём линейно.

Поэтому в выводе мы напишем, что сопротивление проволочного резистора линейно увеличивается с увеличением его длины.

В следующей части работы мы будем исследовать зависимость сопротивления от площади поперечного сечения проводника.

Для выполнения этой работы мы опять используем оборудование из третьего комплекта в составе: источник тока, двухпредельный вольтметр и амперметр, ключ, реостат, соединительные провода и набор проволочных резисторов на подставке.

Прежде чем приступить к работе давайте с вами ещё раз вспомним, что электрическое сопротивление конкретного проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен:

Зависимость сопротивления проводника от площади его поперечного сечения мы с вами и должны будем проверить. Однако для выполнения данной работы эта формула нам не подходит. А, судя по предложенному оборудованию, сопротивление проводника мы будем находить на основании закона Ома для участка цепи:

Итак, приступим к выполнению. Для начала давайте подумаем, какие из проволочных резисторов мы будем использовать в этой работе. Очевидно, что для установления зависимости сопротивления от площади поперечного сечения проводника необходимо выбрать проводники, отличающиеся только диаметром и имеющие одинаковые остальные параметры (длину и материал). Данному условию удовлетворяют два стальных проводника, диаметром 0,3 мм и 0,15 мм.

С проводниками разобрались, теперь соберём экспериментальную установку. Для этого последовательно с источником тока соединим ключ, амперметр на предел измерения 0,6 А, реостат и набор проволочных резисторов так, чтобы в цепь был включён один из стальных проводников (например, тот который потолще). А чтобы измерить напряжение на концах исследуемого резистора, параллельно к нему подключим вольтметр, подключённый на предел измерения 3 В.

Далее мы с вами нарисуем электрическую схему нашей установки.

Теперь запишем формулы, которыми будем пользоваться при выполнении данной работы. Во-первых, запишем формулу для определения сопротивления через геометрические размеры проводника:

Во-вторых, — закон Ома для участка цепи:

А из него находим, что электрическое сопротивление проводника равно отношению напряжения на концах проводника к силе тока в проводнике:

Ещё нам необходимо указать формулу, по которой рассчитывается площадь сечения проводника. Так как проводники у нас имеют цилиндрическую форму, то в их поперечное сечение будет представлять окружность. А из математики мы знаем, что её площадь определяется, как

Прежде чем приступить непосредственно к работе ещё раз внимательно проверьте вашу электрическую цепь. Особое внимание обратите на соблюдение полярности подключения обоих приборов.

Если всё в порядке, то включаем источник питания и замыкаем ключ. Далее, с помощью реостата устанавливаем в цепи заданную нам по условию силу тока.

Установив требуемое значение силы тока, снимаем показания с вольтметра. Итак, у нас напряжение на концах первого резистора оказалось равным примерно 0,2 В. Размыкаем ключ и записываем значение силы тока и напряжения, с учётом погрешности измерений:

Теперь включим в цепь более тонкий стальной резистор и параллельно ему — вольтметр. Замкнём ключ.

Вольтметр показывает нам примерно 0,7 В. Размыкаем ключ. Отключаем источник тока. А результаты измерения напряжения заносим в бланк ответов.

Закончив с прямыми измерениями, приступаем к нахождению сопротивления проводников. Для чего в расчётную формулу поочерёдно подставляем наши значения силы тока и напряжения.

Как видим, сопротивление стального проводника диаметром 0,15 мм больше сопротивления такого же проводника, но диаметром в два раза больше. Поэтому вывод мы напишем так: чем больше диаметр и, соответственно, площадь поперечного сечения проводника, тем меньше его сопротивление.

В последней части работы мы с вами исследуем зависимость сопротивления от удельного сопротивления проводника.

Как и в предыдущих работах мы используем источник тока, двухпредельный вольтметр и амперметр, ключ, реостат, соединительные провода и набор проволочных резисторов на подставке.

Теория у нас остаётся та же.

Только в этот раз нам предстоит проверить зависимость сопротивления проводника от материала, из которого он изготовлен.

Приступаем к выполнению. Давайте посмотрим, какие из проволочных резисторов мы будем использовать в этой работе. Очевидно, что для установления зависимости сопротивления проводника от его удельного сопротивления нам необходимо выбрать проводники, отличающиеся только материалом и имеющие одинаковые остальные параметры (длину и площади поперечного сечения). Данному условию удовлетворяют нихромовый и стальной проводники, диаметром 0,3 мм.

С проводниками разобрались, теперь соберём экспериментальную установку: последовательно с источником тока соединяем ключ, амперметр на предел измерения 0,6 А, реостат и набор проволочных резисторов так, чтобы в цепь был включён один из исследуемых проводников (например, нихромовый). Параллельно к нихромовому проводнику подключаем вольтметр с пределом измерения 3 В.

Далее мы с вами рисуем электрическую схему нашей установки.

Формулы, которыми мы будем пользоваться при этой работы, остались прежними. Это формула для определения сопротивления проводника по его геометрическим размерам:

А также закон Ома для участка цепи, из которого выразим сопротивление:

Проверяем электрическую цепь и, если всё в порядке, включаем источник питания и замыкаем ключ.

С помощью реостата устанавливаем в цепи силу тока в 0,4 А.

Как видим, напряжение на концах нихромового резистора примерно равно 1,2 В. Размыкаем ключ и записываем значение силы тока и напряжения, с учётом погрешности измерений:

Теперь включим в цепь стальной резистор и параллельно ему — вольтметр. Замкнём ключ.

Вольтметр показывает нам примерно 0,2 В. Размыкаем ключ. Отключаем источник тока. А результаты измерения напряжения заносим в бланк ответов.

Далее найдём сопротивления проводников. Для чего в расчётную формулу поочерёдно подставляем наши значения силы тока и напряжения для обоих случаев.

Как видим, сопротивление стального резистора меньше, чем сопротивление нихромового резистора таких же геометрических размеров. Значит в выводе можно написать: чем больше удельное сопротивление проводника, тем больше его электрическое сопротивление.