В данной теме продолжаем решать задачи на тепловые двигатели и коэффициент полезного действия теплового двигателя. В частности подробно остановимся на решении задач, связанных с графиками тепловых процессов.
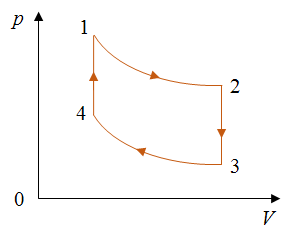
Задача 1. Одноатомный идеальный газ совершает цикл, состоящий из двух адиабат и двух изохор. В процессе адиабатного расширения 1—2 температура газа Т2 = 0,75Т1, а в процессе адиабатного сжатия 3—4 температура газа Т3 = 0,75Т4. Определите КПД цикла.
|
ДАНО:
|
РЕШЕНИЕ
Коэффициент полезного действия цикла
Q1 – количество теплоты, подведенное к газу; Q2 – количество теплоты, отведенное от газа. Теплота к газу подводится в процессе 4–1 в количестве
Теплота отводится от газа в процессе 2–3 в количестве
Тогда КПД цикла
|
|
|
Ответ: КПД цикла составляет 25%.
Задача 2. КПД теплового двигателя, рабочим телом которого является v моль одноатомного идеального газа, равен η. Газ совершает цикл, представленный на рисунке. Разность максимальной и минимальной температур газа в цикле равна ΔТ. Определите работу газа в изотермическом процессе.
|
ДАНО:
|
РЕШЕНИЕ
Коэффициент полезного действия цикла равен
Процесс 1–2 является изотермическим и поэтому
и
Следовательно, из первого закона термодинамики
Процесс 2–3 является изохорным, следовательно работа расширения равна нулю
Тогда из первого закона термодинамики
Тогда КПД
Искомая работа газа равна
|
|
|
Задача 3. На рисунке изображен цикл, проводимый с одноатомным газом. Определите КПД этого цикла.
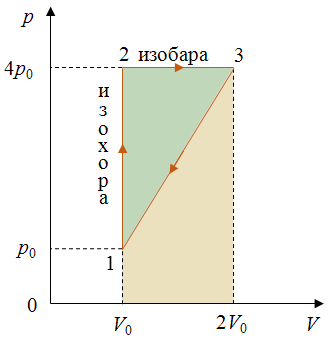
РЕШЕНИЕ
Запишем формулу для расчета коэффициента полезного действия цикла
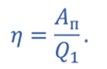
Из графика видно, что при расширении работа, совершаемая газом,
положительна и численно равна площади фигуры, ограниченной графиком 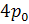 , осью V и отрезками V0–2 и 2V0–3.
, осью V и отрезками V0–2 и 2V0–3.
Работа, совершаемая при сжатии газа в ходе процесса 3–1, отрицательна и численно равна площади фигуры, ограниченной графиком процесса 3–1, осью V и отрезками V0–1 и 2V0–3.
Тогда, полезная работа газа за цикл, равна разности этих площадей

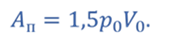
Из графика видим, что в процессе 1–2 происходит изохорное нагревание газа, а в процессе 2–3 — его изобарное расширение. Следовательно, в этих процессах газ получает теплоту
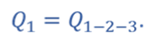
Из первого закона термодинамики следует
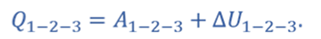
Так как работа газа зависит от вида процесса, то работа 1–2–3 равна сумме работ на участке 1–2 и участке 2–3

При изохорном процессе работа равна нулю
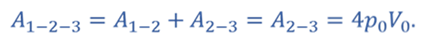
Изменение внутренней энергии


Тогда теплота, подведённая к газу
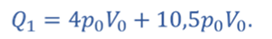
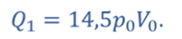
Тогда
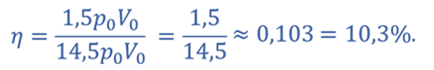
Ответ: КПД цикла равен 10,3%.
Задача 4. Тепловой двигатель, рабочим телом которого является идеальный газ, совершает цикл, изображенный на рисунке. Определите КПД двигателя.
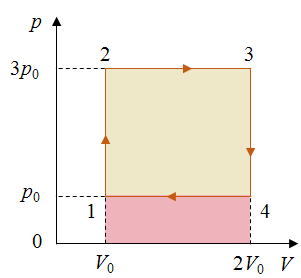
РЕШЕНИЕ
Коэффициент полезного действия цикла
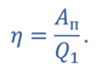
Полезная работа газа
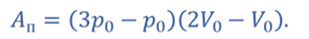

Теплота подводится к газу в изохорном процессе 1–2 и в изобарном процессе 2–3. Согласно первому закону термодинамики эта теплота равна

Работа газа в процессе 1–2–3 равна сумме работ в процессах 1–2 и 2–3

Так как процесс 1–2 изохорный работа расширения газа равна нулю. Тогда работа в процессе 1–2–3
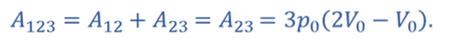

Внутренняя энергия является функцией состояния термодинамической системы и не зависит от того, каким образом система перешла в это состояние. Поэтому изменение внутренней энергии не зависит от вида процессов и равно разности ее значений в конечном и начальном состояниях

Т.к. из уравнения Менделеева-Клапейрона


Тогда количество теплоты, подведенное к газу

Тогда
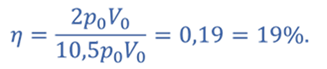
Ответ: КПД двигателя равен 19%.
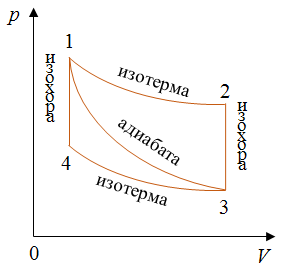
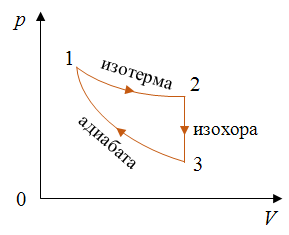
Задача 5. КПД тепловой машины в цикле 1—2—3—1 равен 50%, а в цикле 1—3—4—1 КПД равен 20%. Найдите КПД тепловой машины, работающей по циклу 1—2—3—4.
|
ДАНО:
|
РЕШЕНИЕ Из графика видно, что процессы 1–2 и 3–4 представляют собой изотермы. График процесса 1–3 представляет собой адиабату, так как в этом случае давление газа уменьшается быстрее, чем при изотермическом процессе. Процессы один-четыре и два-три происходят при неизменном объеме газа. Следовательно, это изохорные процессы. Запишем формулу для определения коэффициента полезного действия для цикла 1–2–3–1
КПД для цикла 1–3–4–1
Т.к. процессы 2–3 и 4–1 изохорные, то подведенная теплота расходуется на изменение внутренней энергии. Температура газа в состояниях 1 и 2 одинакова, как и температура газа в состояниях 3 и 4. Следовательно, изменение внутренней энергии в процессах 2–3 и 4–1 одинаковое, а значит Q41 = Q23.
Тогда для цикла 1–2–3–4–1
|
|
|
Ответ: КПД тепловой машины, работающей по циклу 1—2—3—4 равен 40%.

 Получите свидетельство
Получите свидетельство Вход
Вход




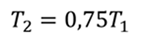
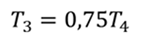
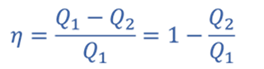
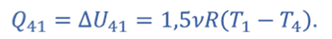
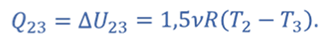

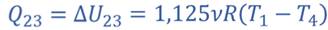
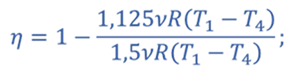
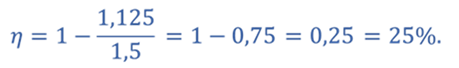
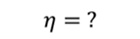
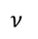
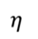
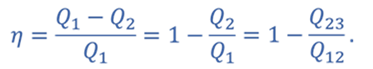
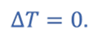



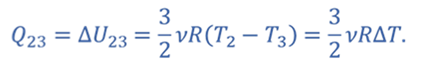
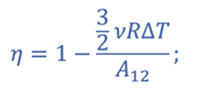
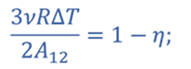
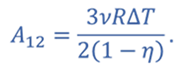
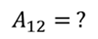
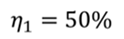
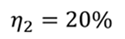
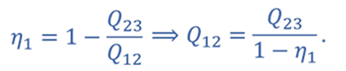
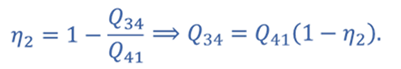
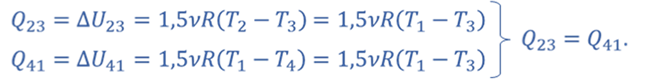
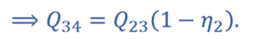
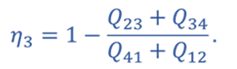
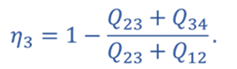
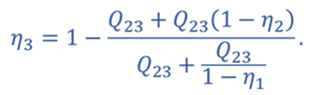
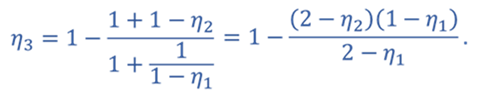
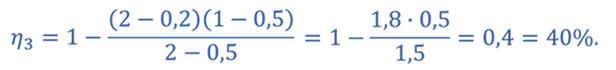
 0
0 18996
18996

