Этапы решение задачи на компьютере. Принцип последовательного конструирования алгоритма

Вопросы:

·     Этапы решения задачи на компьютере.

·     Принцип последовательного конструирования алгоритма.

Давайте подумаем, с чего начинается решение любой задачи, не обязательно связанной с компьютером. Решение любой задачи начинается с прочтения и уточнения её условия. Условия задач мы рассматривали в текстовой форме. Мы выделяли информацию, которая дана в условии – входные данные, а также информацию которую необходимо получить – выходные данные. Это начальный этап решения задачи, то есть её постановка.

После того, как мы определили входные и выходные данные задачи, нам нужно определиться со средствами, которые могут быть необходимы для получения выходных данных из входных. Для этого определяются отношения между ними и записываются на каком-нибудь формальном языке, например, с помощью математических формул. Результатом этих действий будет информационная модель задачи, записанная на некотором формальном языке. Этот этап называется формализацией задачи.

После того, как мы определились со средствами решения задачи, нужно понять, что необходимо сделать для того, чтобы получить выходные данные из входных, какие действия над информацией и в каком порядке для этого нужно произвести. То есть мы составляем алгоритм решения задачи и описываем его одним из известных нам способов, например, с помощью блок-схемы или в текстовой форме. Главное, чтобы было понятно, что должна делать программа и в каком порядке. Этот этап называется созданием алгоритма.

Далее мы записывали созданный алгоритм с помощью языка программирования или других инструментов. И получали компьютерную программу для решения задачи. Этот этап имеет простое название: программирование.

Получив компьютерную программу, мы обычно проверяли правильность её работы. Сначала пробовали запустить программу. После чего задавали несколько различных вариантов входных данных, для которых выходные данные уже были известны, и проверяли, совпадают ли они с теми, которые возвращает программа. Если данные совпадают – программа работает правильно и задача решена. Если же не совпадают – на каком-то из этапов была допущена ошибка. Этот процесс называется тестированием программы.

Ошибки в программе бывают двух видов: синтаксические и логические. Синтаксические ошибки связаны с записью программы на конкретном языке программирования и, как правило, находятся и исправляются средствами среды разработки. Логические ошибки обычно допускаются на более ранних этапах. После того, как ошибка была исправлена, снова проделываются все этапы, следующие за тем, на котором допущена ошибка. Так происходит до тех пор, пока правильность работы программы не подтверждается. Этот процесс называется отладкой.

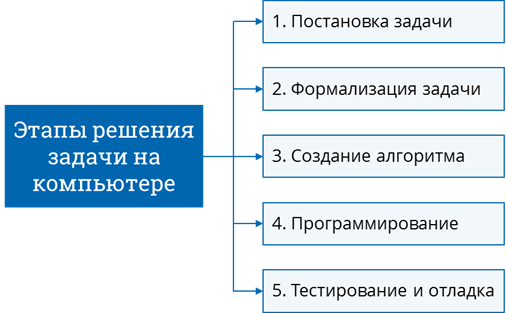
Таким образом, мы выделили пять этапов решения задачи с помощью компьютера: постановка задачи, формализация задачи, создание алгоритма, программирование, тестирование и отладка. Все эти этапы мы выполняли при решении задач и раньше, но для экономии времени часто этапы формализации задачи и создания алгоритма мы объединяли между собой.

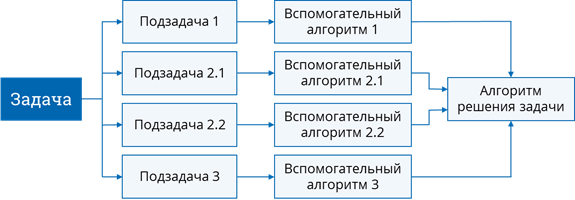
Но предположим, что у нас есть задача, для которой мы уже описали формальную информационную модель, однако придумать алгоритм для решения задачи у нас не выходит, потому что он получается слишком большим и сложным.  Чтобы облегчить эту задачу, можно использовать принцип последовательного конструирования алгоритма, этот принцип также называется «разработкой сверху вниз» или методом «пошаговой детализации». Он состоит в том, что задача разбивается на несколько более простые подзадач, каждая из которых также может разбиваться на подзадачи. Так происходит до тех пор, пока не станет понятным, как решать каждую отдельную подзадачу. Для решения каждой задачи составляется вспомогательный алгоритм. После того, как мы составили вспомогательные алгоритмы для решения всех подзадач, нам остаётся лишь собрать их воедино. Таким образом, мы получим алгоритм для решения исходной задачи.

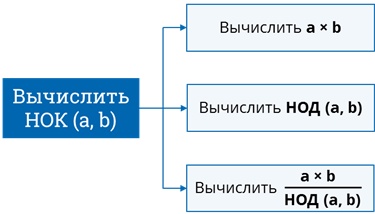
Рассмотрим задачу. Написать программу, вычисляющую наименьшее общее кратное двух целых положительных чисел a и b. Наименьшим общим кратным (НОК) двух натуральных чисел называется наименьшее целое число, которое без остатка делится на оба числа. Из курса математики нам известно, что наименьшее общее кратное двух натуральных чисел можно вычислить как их произведение, делённое на их наибольший общий делитель (НОД). Таким образом, исходную задачу мы можем разбить на 3 подзадачи: вычислить произведение введённых чисел, вычислить их наибольший общий делитель и разделить произведение чисел на их наибольший общий делитель.

Решение первой и третьей подзадач очевидно. Также ранее мы узнали, что наибольший общий делитель двух чисел можно найти, использовав усовершенствованный алгоритм Эвклида, который состоит в том, чтобы заменять большее число в паре его остатком от деления на другое до тех пор, пока одно из чисел не станет равным нулю. После этого ненулевое число будет равным наибольшему общему делителю исходных чисел.

Начнём написание программы для решения задачи. Вначале с помощью инструкции print выведем на экран сообщение о том, что это программа, вычисляющая наименьшее общее кратное целых положительных чисел a и b. С помощью следующей инструкции print выведем на экран запрос на ввод a без перехода на следующую строку. Далее запишем инструкцию для считывания a. Так как по условию задачи a и b – это целые числа, при считывании будем преобразовывать их значения в целочисленный тип int. Теперь скопируем последние две инструкции и изменим их для считывания значения Бэ.

Далее вычислим произведение a и b в переменной p. Таким образом, первая подзадача будет решена. Далее вычислим наибольший общий делитель a и b. Для этого запишем цикл while, который будет повторяться, пока a ≠ 0 и b ≠ 0. Тело цикла будет содержать ветвление, определяющее, какое из чисел наибольшее. Его условием будет: a > b. Если это условие выполняется, то число a на этом шаге цикла наибольшее и согласно алгоритму Эвклида, мы заменим его остатком от деления a на b. Если же условие ветвления не выполняется, то наибольшим числом на этом шаге цикла является b, и мы заменим его остатком от деления b на a. Когда одно из чисел a или b станет равным 0, цикл завершит свою работу и мы вычислим наибольший общий делитель исходных чисел в переменной nod как сумму текущих значений a и b. Таким образом мы решили вторую подзадачу.

Теперь, чтобы вычислить наименьшее общее кратное введённых чисел, присвоим переменной nok значение переменной p, делённое на значение переменной nod. Так как наименьшее общее кратное – целое число, используем для этого операцию целочисленного деления.  Таким образом мы решили третью подзадачу. С помощью инструкции print выведем на экран поясняющее сообщение о том, что наибольшее общее кратное a и b равно значению переменной nok.

print ('Программа, вычисляющая НОК a и b.')

print ('a = ', end = '')

a = int (input ())

print ('b = ', end = '')

b = int (input ())

p = a * b

while a != 0 and b != 0:

    if a > b:

        a = a % b

    else:

        b = b % a

nod = a + b

nok = p // nod

print ('НОК введённых чисел:', nok)

Сохраним написанную программу и протестируем её. Запустим программу на выполнение и зададим числа 2 и 3. Действительно, наименьшее число, которое без остатка делится и на 2, и на 3 – 6. Снова запустим программу и зададим числа 6 и 8. Действительно, наименьшее число, которое без остатка делится и на 6, и на 8 – 24. Программа работает правильно. Задача решена.

Рассмотрим ещё одну задачу. Выпуклый четырёхугольник задан положительными длинами своих сторон: a, b, c и d. Написать программу для вычисления его площади, если известно, что между сторонами a и b прямой угол.

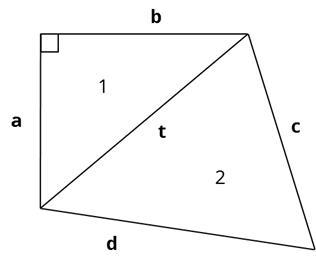
Изобразим условие этой задачи в виде рисунка. Соединим противоположные концы сторон a и b отрезком, длину которого обозначим t. Таким образом мы разделили четырёхугольник на два треугольника со сторонами a, b, t и c, d, t соответственно. Площадь четырёхугольника равна сумме их площадей. Так как между сторонами a и b прямой угол, то площадь первого треугольника можно вычислить как полупроизведение a и b, а t – как гипотенузу первого треугольника. Зная значения c, d и t, мы можем вычислить площадь второго треугольника по формуле Герона. Таким образом, мы записали формулы, необходимые для решения задачи, получив математическую модель.

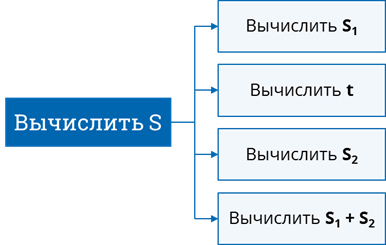
Также мы разобьём задачу на несколько подзадач. Вначале мы вычислим площадь первого треугольника, после чего определим длину стороны t. Далее мы вычислим площадь второго треугольника и в конце рассчитаем площадь четырёхугольника как сумму площадей треугольников, из которых он состоит. Так мы составили алгоритм решения задачи.

Начнём написание программы. Вначале с помощью инструкции print выведем на экран сообщение о том, что это программа, вычисляющая площадь четырёхугольника по длинам его сторон. Угол между сторонами a и b прямой. С помощью следующей инструкции print выведем на экран запрос на ввод a без перехода на следующую строку. Запишем инструкции для считывания значения a. Так как в условии задачи не сказано, что длины сторон – целые числа, при считывании мы будем преобразовывать их значения в вещественный тип float. Скопируем последние две инструкции три раза и изменим их для считывания значений переменных b, c и d. После того как мы рассчитали длины сторон четырёхугольника, вычислим площадь первого треугольника в переменной s1. Для этого присвоим ей значение a * b / 2. Так как для вычисления длины гипотенузы треугольника нам потребуется извлечь квадратный корень, загрузим эту функцию из модуля math в описываемый модуль. После этого вычислим длину гипотенузы первого треугольника в переменной t. Для этого присвоим ей значение квадратного корня из суммы квадратов a и b. Теперь вычислим полупериметр второго треугольника в переменной p. Для этого присвоим ей значение полусуммы c, d и t. Далее вычислим по формуле Герона площадь второго треугольника в переменной s2. Для этого присвоим ей значение квадратного корня из произведения p * (p – c) * (p – d) * (p – t). И, наконец, вычислим площадь четырёхугольника в переменной s, присвоив ей значение суммы s1 и s2. С помощью инструкции print выведем на экран сообщение о том, что площадь четырёхугольника равна значению переменной s. Будем выводить s с точностью в четыре знака после запятой.

print ('Программа, вычисляющая площадь четырёхугольника по длинам его сторон. Угол между a и b прямой.')

print ('a = ', end = '')

a = float (input ())

print ('b = ', end = '')

b = float (input ())

print ('c = ', end = '')

c = float (input ())

print ('d = ', end = '')

d = float (input ())

s1 = a * b / 2

from math import sqrt

t = sqrt (a ** 2 + b ** 2)

p = (c + d + t) / 2

s2 = sqrt (p * (p - c) * (p - d) * (p - t))

s = s1 + s2

print ('Площадь заданного четырёхугольника:', '{:0.4f}'.format (s))

Сохраним описанный модуль и протестируем его. Сначала в качестве четырёхугольника зададим квадрат со стороной, равной 5. Его площадь действительно равна 25. Снова запустим программу на выполнение и зададим четырёхугольник с длинами сторон: 3, 4, 12 и 13. Очевидно, что площадь первого треугольника равна 6, а его гипотенуза – 5. По формуле Герона площадь второго треугольника равна 30. Значит площадь четырёхугольника равна 36. Программа вывела сообщение об этом, это значит, что она работает верно и задача решена.

Мы узнали:

·     Решение любой задачи с помощью компьютера состоит из пяти этапов: постановка задачи, её формализация, создание алгоритма, программирование, тестирование и отладка.

·     Если алгоритм решения задачи сложно придумать сразу, то для этого можно использовать метод последовательного конструирования алгоритма, где задача разбивается на несколько более простых подзадач, каждая из которых также может делиться на подзадачи. Так происходит до тех пор, пока нам не станет понятно, каким образом решить все подзадачи. После этого решения всех подзадач соединяются воедино, образуя алгоритм решения исходной задачи.