Сила упругости

При рассмотрении понятия «сила» мы с вами говорили о том, что она является количественной мерой воздействия одного тела на другое, в результате которого тела приобретают ускорения или деформируются.

Мы уже с вами знаем, что такое ускорение тела. А теперь давайте вспомним, что такое деформация. Итак, под деформацией понимают изменение формы или объёма одного тела в результате воздействия на него другого тела.

Возникновение в теле деформаций объясняется дискретным строением веществ. Вы уже знаете о том, что все вещества состоят из атомов и молекул, разделённых между собой промежутками. Между этими частицами существуют силы взаимодействия электромагнитной природы, которые, в зависимости от расстояния между частицами, проявляются то как силы притяжения, то как силы отталкивания. Например, когда воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению же расстояния между молекулами противодействуют силы отталкивания.

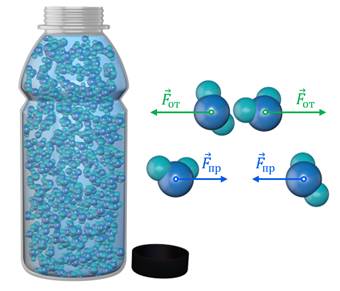
По характеру смещения частей тела (а вернее, молекулярных слоёв внутри него) друг относительно друга различают несколько видов деформации.

Так если расстояние между слоями увеличивается, то говорят о деформации растяжения.

Если же, наоборот, расстояние между слоями уменьшается, то это деформация сжатия.

Деформация, при которой происходит взаимное смещение параллельных молекулярных слоёв под воздействием деформирующей силы, называется деформацией сдвига.

Когда же в разных частях тела возникают неодинаковые комбинации растяжения и сжатия, то это деформация изгиба.

Ну а различные комбинации деформаций сдвига проявляются как деформация кручения.

Также принято различат упругие деформации и неупругие или пластичные.

Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры.

А если этого не происходит, то деформация называется пластичной.

Конечно же, деформация конкретного тела может быть, как упругой, так и неупругой, так как её характер зависит не только от свойств тела, но и от величины воздействия на него, а также от температуры тела. Например, если железную пластину немного изогнуть и отпустить, она восстановит свою форму. Однако если её закрепить в деформированном состоянии на длительное время, то после снятия внешней силы восстановление будет неполным. Если же пластинку нагреть до высокой температуры, то деформация будет пластической даже под действием кратковременной силы.

Чтобы не рассматривать сложные электромагнитные взаимодействия между отдельными частицами вещества, в механике для характеристики этих явлений вводят силы упругости.

Итак, силами упругости называются силы, возникающие при деформации любых твёрдых тел, а также при сжатии жидкостей и газов. Они препятствуют изменению объёма и формы тела.

Следует помнить, что силы упругости приложены к телу, которое вызывает деформацию, и всегда направлены противоположно деформирующей силе перпендикулярно поверхности соприкосновения взаимодействующих тел. Такие силы ещё называют силами реакции опоры. Если же во взаимодействии участвуют такие тела, как пружины или нити, то силы упругости направлены вдоль их оси́ и их называют силами натяжения.

Теперь давайте вспомним с вами, какую роль играет эта сила при взаимодействии тел. Проделаем следующий опыт. Прикрепим к бруску, лежащему на столе, резиновый шнур (с метками на одинаковом расстоянии друг от друга) и медленно начнём тянуть его в горизонтальном направлении. Под действием силы шнур растягивается, и только когда весь шнур растянется на некоторую величину, брусок придёт в движение. Как это объяснить?

Все правильно — при растяжении шнура происходит смещение одних его частей относительно других, в результате чего в шнуре возникает сила упругости, равная по величине деформирующей силе. С этого момента шнур играет роль «передающего звена». Такие же явления всегда происходят, когда движение от одного тела к другому передаётся при помощи «связей», то есть нитей, пружин, тросов, различных сцепок и так далее.

Чаще всего мы с вами сталкиваемся с упругими деформациями растяжения или сжатия. А первое по-настоящему научное исследование этих процессов предпринял Роберт Гук в 1660 году. Он экспериментально установил, что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе.

Проверим это. Возьмём длинную рейку, к которой прикреплены четыре абсолютно одинаковых резиновых шнура. Крайний левый мы будем использовать в качестве эталона. Подвесим ко второму шнуру груз известной массы. Под действием его веса шнур растянется и, следовательно, в нём возникнет сила упругости. Она, согласно третьему закону Ньютона, будет равна по модулю и противоположна по направлению весу тела. А величина удлинения шнура, также называемая абсолютным удлинением, равна разности между его конечной и начальной длиной: ∆𝑙 = 𝑙 − 𝑙₀.

Для третьего шнура увеличим нагрузку в два раза, подвесив на него два одинаковых груза. Шнур растянулся сильнее. При этом видно, что удлинение шнура выросло в два раза.

Наконец, подвесим к последнему шнуру три одинаковых груза. Удлинение шнура выросло в три раза.

Таким образом, действительно, при малых упругих деформациях растяжения или сжатия модуль силы упругости прямо пропорционален абсолютному удлинению тела: F = k|Δl|.

В этом и состоит экспериментально установленный закон Гука.

Коэффициент пропорциональности, входящий в формулу, называют жёсткостью тела. Она численно равна модулю силы упругости при удлинении (или сжатии) тела на единицу длины:

Отметим, что жёсткость является характеристикой данного тела и зависит от материала, из которого оно изготовлено, от формы и размеров тела, а также от его температуры.

При решении большинства задач необходимо помнить, что сила упругости — это всё-таки векторная величина, то есть она имеет направление. Тогда, если выбрать начало отсчёта под крайней точкой недеформированного тела, то абсолютное удлинение можно характеризовать координатой конца деформированного тела.

А так как координата и проекция силы упругости деформированного тела на ось координат имеют противоположные знаки, то закон Гука в проекциях на выбранную ось запишется в виде:

F_{упр х} = –kx.

Ту или иную форму записи закона Гука используют в зависимости от условия задачи и величины, которую нужно определить.

Графиком зависимости силы упругости от абсолютного удлинения тела является прямая линия, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости.

Не забывайте, что закон Гука выполняется только для упругих деформаций, при которых удлинение тела мало!