Расчет скорости, пути и времени движения

Расчёт пути и времени движения

«Движение – это жизнь»

Аристотель

В данной теме будем применять приобретённые знания о механическом движении на практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь – это физическая величина, равная длине траектории, по которой двигалось тело, в течение данного промежутка времени. Путь является скалярной величиной, то есть, не имеет направления. Скорость при равномерном движении – это величина, равная отношению пройденного пути к промежутку времени, за который этот путь пройден.

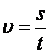
Скорость является векторной величиной, то есть, характеризуется как числовым значением, так и направлением.

Средняя скорость при неравномерном движении – это величина, равная отношению всего пройденного пути к общему времени в пути.

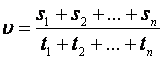
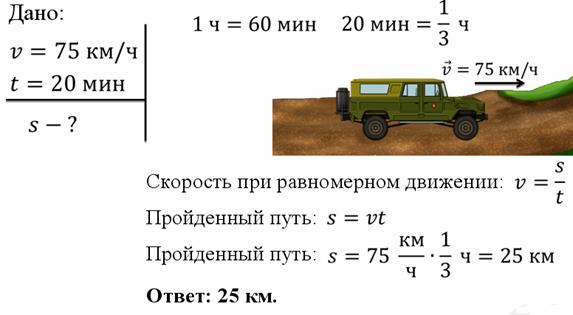
Задача 1. Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?

В первую очередь, необходимо научиться правильно оформлять задачи по физике. При решении любой задачи нужно писать «дано». То есть, в левой части листа необходимо записать слово «дано», после которого ставится двоеточие, а дальше в столбик перечисляете все исходные данные, которые указаны в условии задачи. В нашем случае – это скорость и время в пути. После этого, нужно очеркнуть данные и ниже (уже под линией) записать, что необходимо найти. В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем непосредственно к решению задачи.

А теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть, сколько километров автомобиль проходит за час. А время в условии дано в минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в часы.

В общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами измерения, можно (и даже нужно) переводить данные в систему СИ сразу после того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в км/ч необходимо

                                                      1 м/с = 3,6 км/ч

                                                    1 км/ч = 1/3,6 м/с

Время в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому, чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется переводить данные в систему СИ.

Задача 2. Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.

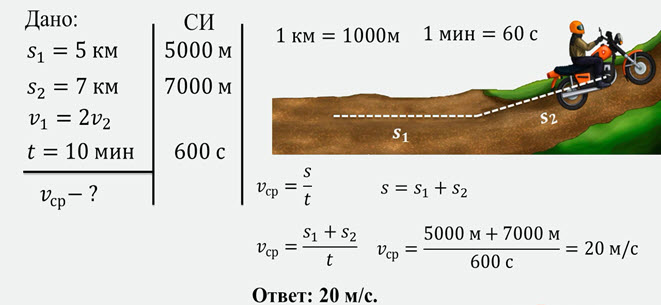
Получившееся выражение, в котором остались, только те величины, которые были даны изначально, называется расчетной формулой. Только в расчетную формулу необходимо подставлять числовые значения, а до этого, все делается в буквенном виде.

Задача 3. Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя скорость?

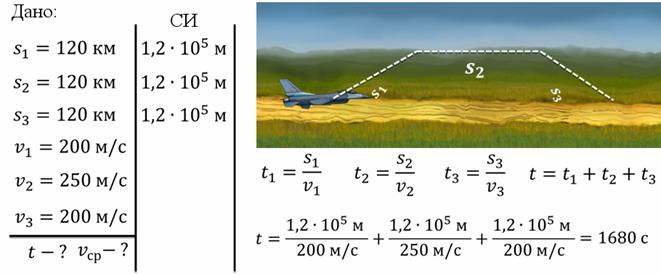
Сразу хочется обратить ваше внимание на распространенную ошибку. Среднюю скорость нельзя находить как среднее арифметическое разных скоростей на разных участках движения. В этом можно убедиться с помощью простых расчетов: если подсчитать среднюю скорость, как среднее арифметическое скоростей, то получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю скорость как отношение всего пройденного пути к общему времени в пути. В результате получим 214,3 м/с. Получается вроде небольшая разница. В результате неверных расчётов за каждую секунду, пройденное расстояние увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное расстоянии будет больше на 8,6 км, а это существенно.

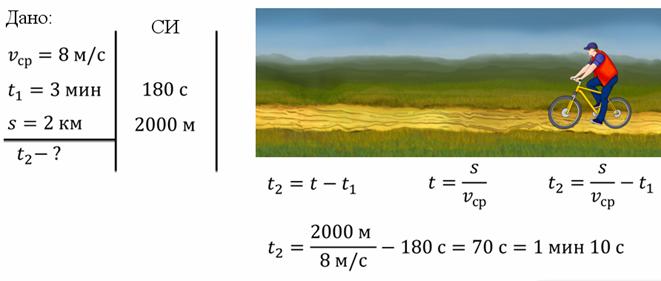
Задача 4. Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть своего пути велосипедист проехал за 3 минуты. За какое время велосипедист проехал вторую часть, если общий путь составил 2 км?

Задача 5. Определите по графику скорость равномерного движения тела.

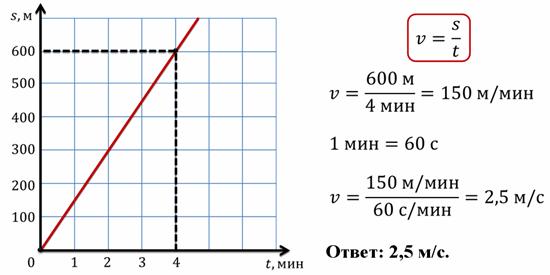
Здесь, конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика: какие величины они обозначают и в каких единицах измеряются. Вертикальная ось – обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах. Значит, это график зависимости пройденного пути от времени. При равномерном движении скорость постоянна, значит, можно путь, пройденный за определенный промежуток времени, разделить на это время и, таким образом, найти скорость. Для наибольшей точности желательно найти точку, на графике, наиболее близкую к пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие координаты, то есть, на значения пути и времени. Для этого из точки опускаем перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.

Основные выводы:

В качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.