Основные формулы и методические рекомендации по решению задач на основы МКТ

Приступаем к рассмотрению новой главы физики «Элементы статистической физики и термодинамики». В данной теме будут рассмотрены некоторые важные определения и понятия, относящиеся к первому ее разделу, который посвящен основам молекулярно-кинетической теории.

Молекулярная физика и термодинамика — это разделы физики, в которых изучаются свойства тел и происходящие в них макроскопические процессы, связанные с огромным числом частиц, содержащихся в телах.

Для исследования этих процессов пользуются двумя методами: молекулярно-кинетическим (его еще называют статистическим методом) и термодинамическим.

В основе молекулярной физики лежит молекулярно-кинетическая теория, которая объясняет строение и свойства тел движением и взаимодействием частиц, из которых состоит тело. При этом она пользуется статическим методом, интересуясь не индивидуальными характеристиками отдельных частиц, а лишь средними значениями физических величин, которые характеризуют движение частиц, составляющих систему.

Термодинамика же изучает общие свойства тел и процессы в них, сопровождающиеся превращениями энергии. То есть процессы, связанные с изменением температуры тела, а также с изменением его агрегатного состояния.

Однако следует помнить, что эти два метода — термодинамический и молекулярно-кинетический, применяемые к одним и тем же объектам, не исключают, а дополняют друг друга.

В основе молекулярно-кинетической теории вещества лежат следующие три положения.

1) Все вещества состоят из мельчайших частиц: молекул, атомов, ионов и других, разделенных между собой промежутками.

Молекула — это мельчайшая устойчивая частица вещества, сохраняющая его основные химические свойства. Однако молекулы, состоят из еще более мелких частиц — атомов. Атомы — это мельчайшие частицы химического элемента, сохраняющие его химические свойства.

Атомы представляют собой весьма сложные образования, но классическая молекулярно-кинетическая теория использует модель атомов в виде твердых неделимых частичек сферической формы.

2) Частицы в веществе связаны друг с другом силами молекулярного взаимодействия — притяжения и отталкивания. Эти силы зависят от расстояния между частицами.

3) Молекулы в веществе находятся в непрерывном беспорядочном (тепловом) движении.

Доказательством теплового движения молекул является броуновское движение.

Именно хаотическое движение молекул газа играет главную роль в его поведении, а силы их взаимодействия настолько малы, что ими можно просто пренебречь. Это означает, молекула газа движется равномерно и прямолинейно, пока не столкнется с другой молекулой. При этом длина свободного пробега молекулы примерно равна 10^–7 м. Такая длина свободного пробега приводит к тому, что лишь 0,04 % пространства, занятого газом, приходится на собственный объем его молекул. Это дает нам право воспользоваться моделью идеального газа.

Идеальный газ — это газ с достаточно простыми свойствами:

1) Собственным объемом молекул можно пренебречь по сравнению с объемом сосуда, в котором находится газ.

2) Между молекулами нет сил взаимодействия; они действуют только при столкновении молекул.

3) Молекулы ведут себя при столкновениях как абсолютно упругие шарики.

Следует отметить, что при небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу.

Для описания свойств газов можно пользоваться микроскопическими параметрами, такими как скорость молекулы, ее масса и энергия, которые являются характеристиками молекул, и средние значения которых находятся только расчетным путем.

А можно пользоваться и макроскопическими параметрами — давлением, абсолютной температурой и объемом.

Под давлением газа понимают среднюю силу ударов его молекул о тело (например, о стенки сосуда), отнесенную к единице поверхности тела.

Абсолютная температура — это мера средней кинетической энергии теплового движения молекулы.

Объем газа — это внутренний объем сосуда, в котором газ находится.

Для связи между макро- и микропараметрами идеального газа пользуются основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение связывает между собой макропараметр p, то есть давление газа, с такими микропараметрами, как средняя квадратичная скорость молекулы или средняя кинетическая энергия молекулы газа.

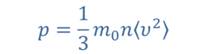
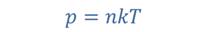
Для связи между макропараметрами, характеризующими состояние идеального газа, используют уравнение состояния.

Если масса газа и его химический состав не изменяется и нужно сравнить два состояния газа, то используют уравнение Клапейрона.

А для любой произвольной массы газа используют уравнение Менделеева — Клапейрона, которое связывает между собой параметры одного состояния газа.

Из уравнения состояния вытекают два важных следствия — это закон Авогадро, и закон Дальтона. Оба этих закона были открыты экспериментально.

Закон Авогадро гласит о том, что при равных давлениях и температурах в одинаковых объемах любых газов содержится одинаковое число молекул.

Закон Дальтона, что давление смеси газов равно сумме парциальных давлений каждого из газов в отдельности.

Процессы, при которых один из параметров «давление», «температура» или «объем» остается постоянным, называют изопроцессами. Стоит отметить, что законы, описывающие изопроцессы в идеальном газе, были открыты задолго до создания молекулярно-кинетической теории идеального газа.

Изотермический процесс – это процесс изменения состояния газа при постоянной температуре.

Графики зависимости между параметрами данной массы газа при постоянной температуре называются изотермами.

Для изотермического процесса справедлив закон Бойля — Мариотта: при постоянной температуре, неизменной массе и неизменном химическом составе газа произведение давление на объем есть величина постоянная.

Процесс изменения состояния газа при постоянном объеме называется изохорным процессом.

Графики зависимости между параметрами газа при постоянной массе газа и постоянном объеме называют изохорами.

Для изохорного процесса справедлив закон Шарля: давление данной массы газы при постоянном объеме и неизменном химическом составе прямо пропорционально абсолютной температуре.

Если изменение состояния газа происходит при постоянном давлении, то данный процесс называют изобарным.

Графики зависимости между параметрами газа при постоянной массе газа и постоянном давлении называют изобарами.

Для изобарного процесса применим закон Гей-Люссака, согласно которому, объем данной массы газы при постоянном давлении и неизменном химическом составе прямо пропорционален абсолютной температуре.

Теперь представим основные формулы в виде таблицы.

Методические указания по решению задач.

1) Выяснить, изменяется ли состояние газа.

2) Если в задаче даны два или несколько состояний газа, то следует отдельно выписать параметры этих состояний.

3) Если это возможно, то сделать схематический рисунок.

4) выяснить, изменяется ли масса газа.

5) Если масса газа изменяется или дана в условии задачи, то для каждого состояния необходимо записать уравнение Менделеева — Клапейрона.

6) Аналогично поступаем и тогда, когда по условию задачи изменяются состояния двух и более газов, разделенных между собой перегородкой, поршнем и так далее.

7) Если масса газа не изменяется, то необходимо будет записать уравнение Клапейрона или один из трех законов для изопроцессов: Бойля — Мариотта, Шарля или Гей-Люссака.

8) Представить в развернутом виде параметры начального и конечного состояний газа.

9) При необходимости, надо записать и вспомогательные уравнения, связывающие искомые величины или параметры состояния, используя условие задачи.

10) решить полученную систему уравнений относительно неизвестных величин в общем виде и проверить правило размерностей. Получить результат в численном виде.