На этом уроке мы с вами узнаем такие понятия, как натуральные числа, число 0 (нуль), натуральный ряд. Поговорим о свойствах натуральных чисел. Рассмотрим виды систем счисления. А также обсудим знаки для записи системы счисления.
Человек выражает свои чувства, эмоции и отношение к чему-либо или к кому-либо с помощью слов. Все вы, обращаясь друг к другу, используете слова.

В математике также существует свой язык, и выявляется он не только словами, но и числами.
Натуральные числа – одно из старейших математических понятий. У древних людей кроме топора, сделанного из камня, и одежды из шкуры ничего не было, поэтому считать им было нечего. Со временем они стали приручать животных, обрабатывать поля, и появилась торговля.

Тут уж без счёта им стало не обойтись. Сначала считали на пальцах. Когда пальцев одной руки не хватало, переходили на пальцы второй руки, а если считать нужно было дальше и пальцев обеих рук не хватало, то переходили на пальцы ног.

Чисел очень много, поэтому математики разбили их на несколько групп. Самая маленькая из них – натуральные числа.
С помощью натуральных чисел мы можем говорить о количестве предметов, а также можем назвать порядковый номер во множестве предметов.
Вот, к примеру, давайте посчитаем, сколько яблок на картинке.

Одно, два, три, четыре, пять.
Сейчас мы говорили о количестве предметов.
А если вспомнить урок физкультуры, когда учитель просит вас рассчитаться в строю, то, наверняка, каждый из вас может без особого труда назвать свой номер.

Здесь мы уже говорим о порядковом номере каждого ученика в строю.
Определение
Числа, которыми мы с вами пользовались при счёте, называют натуральными числами.
Обозначают их латинской
буквой 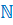 .
.
Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин:
· длины,
· площади,
· времени,
· скорости.

Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным!
С натуральными числами можно выполнять следующие арифметические действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
Чтобы человек мог использовать натуральные числа, они должны быть каким-либо образом понятны нашему слуху, а также зрению.
Если озвучить каждое натуральное число, то оно станет слышно.

А если изобразить натуральное число, то его можно будет увидеть. Это самые простые способы воспринять натуральные числа.
Записывать числа люди научились гораздо позже, чем считать. Раньше всего они стали изображать 1 одной палочкой, 2 – двумя палочками, 3 – тремя палочками и так далее с остальными числами.
В Древней Греции поступали гораздо проще: греки не стали выдумывать специальные знаки для цифр, а использовали вместо них буквы.
1 обозначали буквой А, цифру 2 обозначали буквой Б и так далее с остальными числами.
Цифры, которыми мы пользуемся для записи чисел, родились в Индии несколько тысячелетий назад. В Европу их привезли арабы, поэтому их стали называть арабскими цифрами.
Однако в самой Индии до последнего времени цифры выглядели совсем не так, как в Европе. Затем появились и особые знаки для обозначения чисел — предшественники современных цифр.
Кстати, «нуль» по арабски – «сифр», откуда и пошло название «цифра».
Для счёта предметов используют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр. Давайте назовём их:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Посмотрите, как мы записываем числа.
К примеру, число «пятьсот двадцать один» – 521.
Или «двадцать тысяч пятьсот» – 20 500.
Такой способ записи чисел, которым мы пользуемся, называется десятичной позиционной системой счисления. Числа в ней записываются с помощью десяти цифр. Значение цифры зависит от её места (позиции) в записи числа.
Возьмём, например, числа 250 и 502.
В первом числе цифра 5 обозначает количество десятков.
В записи числа 502 цифра 5 уже обозначает количество сотен.
Цифра 0 в записи обоих чисел указывает на отсутствие единиц в разряде.
Определение
Все натуральные числа, записанные по порядку (каждое число на своём месте), образуют натуральный ряд.
В натуральном ряду на первом месте стоит цифра 1, а каждое последующее число на единицу больше. Т. е., чтобы получить 2, мы должны к 1 + 1. Чтобы получить 3, мы точно так же будем к 2 + 1 и т. д.
Скажите, пожалуйста, до какого числа мы можем с вами посчитать? Назовите любое большое число. А какое число больше его на 1?
Получается, что самого последнего числа нет, т. к. к имеющемуся последнему числу можно прибавить единицу и снова получить новое последнее число. Перечисление натуральных чисел не имеет конца, и поэтому говорят, что натуральный ряд бесконечен. Весь натуральный ряд записать НЕВОЗМОЖНО! Поэтому поступают следующим образом: записывают подряд несколько последовательных чисел, начиная с 1, после чего ставят многоточие.
1, 2, 3, 4, … .
Первым натуральным числом является 1(единица), а вот последнего числа не существует.
Итак, теперь давайте выявим свойства натурального ряда.
Свойства натурального ряда:
1) наименьшее число натурального ряда – 1(один), наибольшего нет;
2) для каждого числа найдётся такое, которое больше его на 1;
3) для каждого числа, кроме 1, найдётся такое, которое меньше его на 1;
4) число 0 «нуль» не является натуральным, поскольку не используется при счёте.
Эти четыре правила нужно запомнить, поскольку они необходимы при решении многих задач.
Рассмотрим несколько примеров правильной записи натуральных чисел. Перед нами четыре числа:
22, 3 476, 5 000, 120 540
Из приведённых примеров можно заметить, что для того чтобы записать натуральное число, не обязательно нужно использовать все из десяти цифр, а ещё цифры в записи числа могут повторяться. Вот, например, число 22: здесь цифра 2 повторяется.
Посмотрите на следующие записи чисел:
07, 0005, 0406
Они не являются записями натуральных чисел, т. к. слева находится цифра 0 (нуль). Запомните: запись натурального числа в десятичной системе счисления НЕ МОЖЕТ начинаться с нуля.
Помимо десятичной системы счисления существуют и другие. Например, в информатике используется двоичная позиционная система счисления.
А с шестидесятеричной системой счисления мы сталкиваемся, когда говорим об измерении времени.

Существуют и непозиционные системы счисления. Например, римская нумерация. В ней числа записываются с помощью римских цифр. Посмотрите, как обозначаются римские цифры:

Для записи римских чисел используются правила сложения и вычитания. Если меньшая цифра стоит после большей, то она прибавляется к большей, а если меньшая цифра стоит перед большей, то она вычитается из большей.
Примеры
Посмотрите, как правильно называть число в римской нумерации.
Например, число ІІІ.
Здесь все цифры равноценны. Значит, мы будем просто складывать единицы:
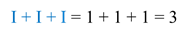
Дальше — число VІІ.
В этом числе стоит на первом месте цифра 5. Она больше единичек, записанных после неё. Т. е. получаем, что меньшие цифры стоят после большей, а значит, мы будем прибавлять:

Посмотрим следующее число: XXI.
Здесь точно так же меньшая цифра стоит после больших. Значит, по правилам записи римских чисел будем складывать:
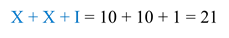
Следующее число: IV.
В этом числе меньшая цифра записана перед большей. Следовательно, мы должны от большего отнять меньшее:
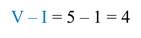
Следующее число: IX.
Здесь точно так же меньшая цифра стоит перед большей. Значит, будем от большего числа отнимать меньшее:
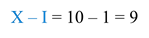
Римскую нумерацию сейчас используют только для записи порядковых числительных. Так, например, запись «XXI в.» читают: «двадцать первый век». А запись «V класс» читают: «пятый класс».
Итоги
Итак, на уроке мы познакомились с такими понятиями, как натуральные числа, число 0 (нуль), натуральный ряд, а также изучили свойства натурального ряда. Узнали, какие бывают системы счисления, с помощью каких знаков они записываются.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 6039
6039

