Два, четыре, шесть, восемь, десять.

Ну, что, я вас напугал? Нет? Вот незадача! Я ведь домовой в царстве математики, и должен вас пугать. Но мне никогда не удаётся никого напугать. Ладно, не удалось испугать – придётся дружить. Здравствуйте, ребята! Меня зовут Матеша…ой, то есть Матвей, Матюша. А так как я предлагаю вам подружиться со мной, то, конечно, буду помогать вам – проводить экскурсии по нашей замечательной стране. Я ведь самый лучший в мире знаток математики – знаю в нашей стране каждую щёлочку, каждый закоулочек. Ну конечно, если честно, наша царица Математика лучше разбирается во всем. Но, и я все-таки тоже не лыком шит.
А сегодня я совсем не случайно играл с шариками. Вы обратили внимание, как появлялись шарики – парами. Сначала два, потом ещё два. Их стало четыре. Ещё два – шесть, восемь, десять.
Вы знаете, эти шарики я хочу подарить моим друзьям – Плюсу и Минусу. А вот как я это буду делать. Если бы у меня был один шарик, я бы никак не смог разделить его между ними. А вот если шариков два – один дам Плюсу, один – Минусу. Три шарика на двоих поровну не разделишь – один будет лишний или, наоборот, одного не будет хватать. Добавим один. Шаров стало четыре. А четыре разделить на два поровну очень просто – два Плюсу и два – Минусу. Если бы шариков было пять – опять поровну не разделишь. Один остался бы. Добавляем ещё один – их становится шесть. Каждому по три. Семь шариков – вновь один остаётся. Добавляем один. Шариков восемь – делим поровну по четыре. Девять шариков поровну на двоих не разделишь. Опять один остаётся. А десять делим – получается поровну, по пять шариков.

Вот как интересно получается. Есть числа, которые можно разделить на две равные части, а есть такие, которые нельзя. В них всегда один остаётся. В математике говорят так: один в остатке.
Если посмотреть на числовой луч, то числа располагаются вот в таком порядке:

Видите, те числа, которые делятся на два поровну, чередуются с теми, которые при делении на два дают в остатке один.
У нас в математике такие числа, которые можно разделить поровну на два, называются чётными. А те, которые нельзя так разделить – нечётными. У нечётных чисел всегда одна единичка лишняя. Но стоит её убрать или добавить ещё одну единичку, как число становится чётным.

Давайте вспомним таблицу умножения числа два.
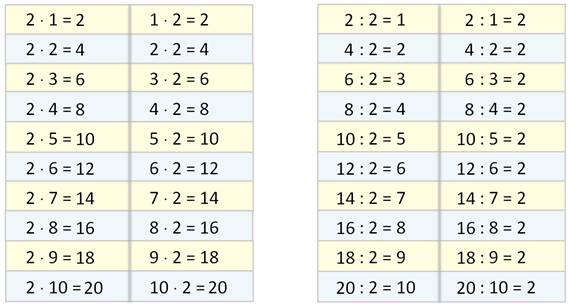
Посмотрите на ответы этой таблицы. При умножении числа два или на два, все ответы – чётные числа. А теперь посмотрите таблицы деления на два и с ответом два. В них все уменьшаемые тоже чётные числа. Ведь на два поровну могут делиться только чётные числа.
А теперь я предлагаю вам расположить все числа в пределах десяти вот в таком порядке.

Видите, что все числа, которые делятся на два, заканчиваются цифрами два, четыре, шесть, восемь или нулём. Давайте продолжим эти ряды.
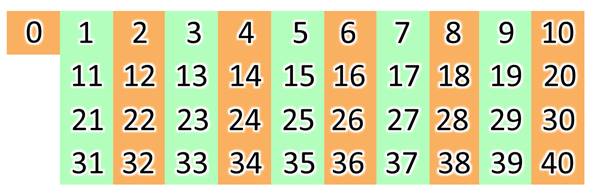
И опять, как видите, чётные числа заканчиваются именно на эти цифры. Кстати, конечно, разделить нуль шариков на две равные части у нас не получится – делить-то нечего. Но всё равно в математике число нуль считается чётным. Потому что на нуль заканчиваются такие чётные числа, как десять, двадцать, тридцать, сорок и так далее. То есть все числа, которые заканчиваются на нуль будут чётными.
Ну а если записать вот такое огромное число один миллион триста пятьдесят семь тысяч девятьсот тридцать, мы можем, не задумываясь, сказать, что это число чётное. Потому что оно заканчивается цифрой нуль. А если такое число? Девятьсот семьдесят два? Оно тоже чётное. Ведь оно заканчивается цифрой два. А вот число 39 тридцать девять – нечётное. Ведь оно заканчивается цифрой девять. А девять – нечётное число.
Ну что, вы поняли, ребята, какие числа называются чётными, а?
Числа, которые можно разделить на два, называются чётными.
Числа, которые нельзя разделить на два, называются нечётными.
Чётные числа заканчиваются цифрами 0, 2, 4, 6, 8.
Нечётные числа заканчиваются цифрами 1, 3, 5, 7, 9.
Уффф, устал. Всё, я прячусь. Пока, ребята.

 Получите свидетельство
Получите свидетельство Вход
Вход




 3849
3849

