Электромагнитная индукция. Опыты Фарадея

На прошлых уроках мы с вами говорили о магнитном поле и его характеристиках. Давайте вспомним, что магнитное поле — это силовое поле, возникающее при движении электрических зарядов независимо от рода проводника или среды, в которой эти заряды движутся.

А силовой характеристикой магнитного поля является вектор магнитной индукции, направление которого в данной точке совпадает с направлением силовой магнитной линии, проходящей через эту точку:

Но проблема в том, что магнитная индукция характеризует магнитное поле в конкретной точке пространства. А очень часто нам необходимо знать характеристики магнитного поля во всех точках пространства, ограниченного замкнутым контуром. Для этих целей вводят физическую величину, называемую магнитным потоком (или потоком магнитной индукции).

Что мы понимаем под потоком в обычной жизни? Кто-то подумает о потоках воды в реке, а кто-то о ветре — потоках воздуха. Аналогично и с магнитным потоком, который можно рассматривать как величину, пропорциональную числу магнитных линий, проходящих через площадь, ограничивающую некоторую поверхность.

Итак, магнитным потоком через плоскую поверхность, находящуюся в однородном магнитном поле, называют скалярную физическую величину, равную произведению модуля индукции магнитного поля, площади поверхности, ограниченной контуром, и косинуса угла между направлениями нормали к этой поверхности и магнитной индукции:

В системе СИ за единицу магнитного потока принят вебер, названный так в честь немецкого учёного Вильгельма Эдуарда Вебера, главные работы которого посвящены изучению магнитных явлений и электричества:

Анализ определения показывает, что изменить магнитный поток через поверхность, ограниченную контуром, можно тремя способами:

изменяя индукцию магнитного поля, в котором находится контур: очевидно, что чем больше индукция магнитного поля, тем гуще линии магнитной индукции, и тем больший магнитный поток пронизывает контур;

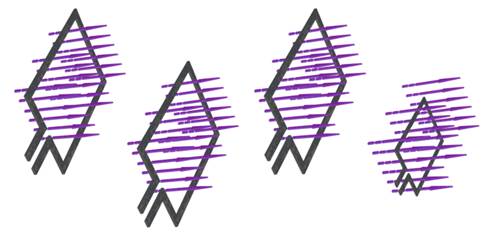
изменяя размеры этого контура: при том же значении магнитной индукции магнитный поток, пронизывающий контур большей площади, будет больше;

а также меняя ориентацию контура в магнитном поле. При этом очевидно, что в случаях, когда линии магнитной индукции перпендикулярны плоскости контура, магнитный поток достигает своего максимума. А в случае, когда плоскость контура параллельна линиям индукции, магнитный поток равен нулю.

Но вернёмся к магнитной индукции. После опытов Эрстеда и Ампера стало понятно, что электрические и магнитные поля имеют одни и те же источники — движущиеся электрические заряды. Это навело многих учёных на мысль о том, что электрические и магнитные поля должны быть взаимосвязаны друг с другом. Великий английский учёный Майкл Фарадей в начале 1822 года в своём дневнике оставил такую запись: «Превратить магнетизм в электричество!»

Рассуждения учёного были следующими: если в опыте Эрстеда электрический ток обладает магнитной силой, а, по убеждению Фарадея, все силы взаимопревращаемы, то и движение магнита должно возбуждать электрический ток.

Спустя 10 лет, а именно 29 августа фундаментальная задача была решена. В период с 29 августа по 4 ноября 1831 года (то есть спустя почти десять лет) Майкл Фарадей провёл серию опытов, позволивших ему сделать величайшее открытие того времени. Рассмотрим некоторые из них.

Итак, для начала давайте с вами соберём чувствительную цепь, состоящую из источника тока, двух катушек разного диаметра, гальванометра и ключа. Одну катушку мы подключим к источнику тока. А концы второй катушки соединим с гальванометром. Вставим одну катушку внутрь второй. Наблюдая за гальванометром, замкнём ключ — стрелка отклоняется на несколько делений, а затем возвращается в исходное положение. Движение стрелки говорит нам о том, что по виткам внутренней катушки прошёл кратковременный электрический ток. А теперь разомкнём цепь — по катушке вновь протекает ток, но уже в обратном направлении.

Повторим опыт, но теперь оставим ключ в замкнутом положении, а катушку, соединённую с гальванометром, будем перемещать относительно первой катушки. Не трудно заметить, что при движении катушки в цепи протекает ток. Фарадей также заметил, что если перемещать катушку, соединённую с источником тока, оставляя вторую катушку неподвижной, то результат будет тот же.

Эти наблюдаемые Фарадеем мгновенные вторичные токи, которые вызываются влиянием первичных токов, были названы им индукционными токами, то есть наведёнными.

Но учёный не остановился на достигнутом и решил выяснить, не влияет ли на появление индукционных токов источник тока? 17 октября 1831 года он ставит свой решающий эксперимент:

«Я взял цилиндрический магнитный брусок и ввёл один его конец внутрь спирали из медной проволоки, соединённой с гальванометром. Потом я быстрым движением втолкнул магнит внутрь спирали на всю его длину, и стрелка гальванометра испытала толчок. Затем я так же быстро вытащил магнит из спирали, и стрелка опять качнулась, но в противоположную сторону. Эти качания стрелки повторялись всякий раз, как магнит вталкивался или выталкивался». Но вот вращение магнита внутри катушки не вызывало появление индукционного тока.

«Ток возникает лишь при движении магнита относительно провода, а не в силу свойств, присущих ему в покое», — записал Фарадей в свой научный дневник.

Что бы убедиться в своих выводах, Фарадей проделал ещё несколько опытов. В одном из них он поместил в магнитное поле плоский контур, концы которого были соединены с гальванометром. Когда контур приводился во вращение, стрелка гальванометра отклонялась, то в одну, то в другую сторону, фиксируя появление индукционного тока. Ток возникал и тогда, когда рядом с контуром или внутри него приводился во вращение постоянный магнит.

И несмотря на то, что рассмотренные нами опыты внешне выглядят различно, Фарадей уловил в них нечто общее — то, от чего зависит возникновение индукционного тока. А именно в замкнутом проводящем контуре индукционный ток возникает только тогда, когда изменяется число линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.

Чуть ранее мы с вами показали, что число линий индукции, пронизывающих рамку, определяет магнитный поток. Поэтому можно сказать, что при всяком изменении магнитного потока, пронизывающего замкнутый проводящий контур, в этом контуре возникает индукционный ток, существующий в течение всего времени изменения магнитного потока. В этом и состоит суть явления электромагнитной индукции.

Открыв явление электромагнитной индукции, Фарадей буквально за полтора месяца установил все его существенные закономерности. Ему стала понятна сущность явления, которое сыграло такую важную, без преувеличения, роль для всего человечества: во всех проведённых опытах индукционный ток в проводящем контуре возникал только в результате изменения магнитного потока через поверхность, ограниченную этим контуром.

Однако оставался не решённым ещё один очень важный вопрос: каково направление возникающего индукционного тока? Ответ на него получил петербургский академик Эмилий Христианович Ленц в 1833 году. Проведя серию экспериментов по исследованию явления электромагнитной индукции он установил, что возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, противодействует изменению магнитного потока, которым вызывается этот индукционный ток.

Правило Ленца можно проиллюстрировать на таком опыте. Возьмём два лёгких алюминиевых кольца, находящихся на острие подставки. Одно кольцо, как видно, сплошное. Другое же кольцо имеет небольшой разрез. Теперь возьмём постоянный магнит и попробуем приблизить его к разрезанному кольцу. Как видим, разрезанное кольцо никак не реагирует на магнит. Это говорит нам о том, что индукционный ток в этом кольце не возникает.

А теперь попробуем приблизить магнит к сплошному кольцу. Как видим, оно отталкивается от магнита, подобно тому, как отталкиваются два одноимённых полюса магнита. И действительно, когда мы пытаемся внести магнит в кольцо, то в последнем возникает индукционный ток, который порождает собственное магнитное поле. По правилу Ленца это поле имеет такое направление, что линии его индукции направлены противоположно линиям индукции внешнего поля магнита. Иными словами, кольцо и магнит оказываются обращёнными друг к другу одноименными полюсами.

Продолжим наши опыты. Но теперь, придерживая коромысло рукой, внесём магнит в сплошное кольцо. Отпустив коромысло, попробуем вытянуть магнит — кольцо следует за магнитом, подобно тому, как притягиваются два разноимённых полюса магнита. Объясним и этот случай. Когда мы пытаемся убрать магнит из кольца (то есть уменьшаем магнитный поток), то в кольце вновь возникает индукционный ток, но уже другого направления. Этот ток также порождает собственное магнитное поле.  Однако линии индукции этого поля теперь направлены так же, как и линии индукции внешнего поля магнита. Иными словами, кольцо и магнит оказываются обращёнными друг к другу разноимёнными полюсами.

В более сжатой форме правило Ленца можно сформулировать следующим образом: индукционный ток всегда направлен так, что его действие противоположно действию причины, вызвавшей этот ток.

Индукционный ток, как и всякий ток, обладает энергией. Следовательно, получая индукционный ток, мы тем самым получаем электрическую энергию. Согласно закону сохранения и превращения энергии, последняя может быть получена только за счёт эквивалентного количества энергии какого-нибудь другого вида.

Когда мы приближаем, например, к катушке магнит, то возникающий в ней индукционный ток своим магнитным полем отталкивает магнит. Двигая магнит, мы преодолеваем эти силы отталкивания, то есть совершаем работу, в результате чего механическая энергия и превращается в энергию индукционного тока.

При выдвигании магнита из катушки совершается работа по преодолению силы притяжения катушки. Механическая энергия здесь также превращается в энергию индукционного тока. Таким образом, закон Ленца находится в полном соответствии с законом сохранения и превращения энергии.

Для того, чтобы определить направление индукционного тока по правилу Ленца, необходимо выполнить несколько действий. Для начала необходимо выяснить, как направлены линии магнитной индукции внешнего магнитного поля. Затем нужно установить, увеличивается или уменьшается магнитный поток через поверхность, ограниченную проводящим контуром. После этого мы должны определить направление линий индукции магнитного поля индукционного тока. Для этого необходимо руководствоваться следующим: если изменение магнитного потока является величиной отрицательной, то направления индукций внешнего магнитного поля и магнитного поля индукционного тока совпадают, в противном случае эти направления противоположны. И, наконец, узнав направление линий индукции магнитного поля индукционного тока, воспользоваться правилом буравчика для определения направления индукционного тока.

В заключении урока отметим, что наибольшего значения индукционные токи достигают в массивных проводниках. Такие токи принято называть токами Фуко по имени исследовавшего их французского физика Жана Бернара Фуко. Как правило, эти токи используются для нагревания проводников, например, в индукционных печах, современных индукционных плитах и так далее.

Однако существует много устройств, в которых возникновение токов Фуко́ приводит к бесполезным, а порой и нежелательным потерям энергии на выделение тепла. Поэтому, например, в электродвигателях, генераторах, и трансформаторах железные сердечники выполняются не из сплошного металла, состоящие из отдельных пластин, изолированных друг от друга.