Представим себе такую историю.
– Да сколько же их ещё спряталось? – задумался Саша.
– Саша, что ты там так усердно ищешь? – поинтересовался Паша.
– Мама мне купила конфеты, а я случайно рассыпал пакет, – расстроенно ответил Саша. – Нашёл всего лишь 12. Вот теперь думаю, сколько же мне ещё нужно найти конфет.
– А сколько всего конфет тебе купила мама? – уточнил Паша.
– 18! – ответил Саша.
– Надо подумать, – задумался Паша. – Помнишь, нам Электроша рассказывал, как складывать натуральные числа? Сейчас у тебя есть 12 конфет. Чтобы их стало 18, мы должны к 12 добавить ещё 6 конфет. Правильно?
– Точно! И как я сам до этого не додумался! – обрадовался Саша. – Значит, у меня тут ещё где-то затерялись 6 конфет. Когда знаешь их количество, то проще искать. Интересно, а есть ли ещё какие-нибудь способы узнать, сколько конфет я потерял?

– Я думаю, Электроша сможет нам помочь! – предложил Паша.
– Ребята, прежде, чем я вам расскажу о вычитании чисел, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим о вычитании натуральных чисел, – предложил Электроша. –Вычитание является действием, обратным для сложения.
– Как это понимать? Обратное действие? – спросили ребята.
– Чтобы ответить на ваш вопрос, давайте вернёмся к конфетам, которые искал Саша. 18 конфет – это сумма двух чисел, одно из которых равно 12 (это те конфеты, которые нашёл Саша), а другое число неизвестно, то есть неизвестно, сколько конфет Саше ещё нужно было найти.
Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое, называют вычитанием. Поэтому вычитание и называют обратным действием сложению.
Паша правильно догадался, что для того, чтобы выяснить, сколько конфет ещё не найдено, нужно найти такое число, которое в сумме с числом 12 даст число 18. И таким числом является 6. То есть Саше осталось найти ещё 6 конфет.
Записывают вычитание следующим образом: 18 – 12 = 6.
На языке математики вычитание записывают так: если от натурального числа а отнять натуральное число b, только если а не меньше, чем b, то в результате получится новое натуральное число c. В этой записи буквами обозначены числа. Вообще, равенство а – b = c верно, если верно равенство b + c = а.

Запомните! Число, от которого отнимают, то есть которое будут уменьшать, называют уменьшаемым. Число, которое отнимают, то есть вычитают, называют вычитаемым. Число, которое получают в результате вычитания, называют разностью.
Так, в наших примерах, в записи 18 – 12 = 6, число 18 – это уменьшаемое, число 12 – вычитаемое, а число 6 – разность. Кстати, саму запись 18 – 12 тоже называют разностью. Точно так же и в равенстве а – b = c: число а называют уменьшаемым, число b – вычитаемым, число c и запись а – b – разностью.

– Слово «разность» очень похоже на слово «разница», – перебил Паша.
– Ты правильно заметил, – подтвердил Электроша. – С одной стороны, разность – это результат вычитания из большего числа меньшего. А с другой, – разность показывает, на сколько первое число больше второго или на сколько второе число меньше первого, то есть показывает разницу между числами. При действиях с натуральными числами уменьшаемое всегда должно быть больше вычитаемого.

А теперь давайте попробуем найти разность чисел 50 254 и 3164.
– Ого! Какие большие числа! – удивились ребята. – Тут нам без калькулятора не обойтись.
– Ребята, всё гораздо проще, чем кажется на первый взгляд, – успокоил ребят Электроша. – Для вычитания многозначных натуральных чисел используют вычитание столбиком. Такой способ поможет быстро и без ошибок выполнить вычисление.
– Итак, для того, чтобы отнять от одного многозначного числа другое столбиком, запишем два числа одно под другим таким образом, чтобы цифры соответствующих разрядов оказались на одном уровне, то есть единицы записываем под единицами, десятки – под десятками, сотни – под сотнями и так далее. Обратите внимание, уменьшаемое обязательно записываем сверху. Под нижним числом проведём черту, а слева от записанных чисел поставим знак вычитания – минус. Затем мы с вами будем вычитать цифры в каждом разряде, начиная с младшего разряда (самого правого).
В наших числах, в разряде единиц записаны четвёрки. От 4 отнимем 4 – получим 0. Результат запишем под тем разрядом, в котором выполнено вычитание.
Дальше в разряде десятков у нас записаны числа 5 и 6.
– Электроша, но ведь 5 меньше 6! – заметили ребята, – мы не можем выполнить такое вычитание.
– Если вдруг из одного числа нельзя вычесть второе, то нужно занять десяток у соседней цифры слева. А над самой цифрой поставить точку, чтобы не забыть, что у этой цифры мы одолжили 1. То есть мы у соседней двоечки занимаем 1 десяток и добавляем к 5. Получаем 15. Теперь мы можем от 15 отнять 6. Получим 9. Запишем результат под разрядом десятков.
Переходим к разряду сотен. Здесь у нас записаны цифры 2 и 1, но точка над двойкой нам напоминает, что единичку у двоечки мы уже заняли. Значит, осталась 1. 1 минус 0 – получим 0.
Выполняя таким же образом вычитание соседних цифр, в итоге получим 47 090.

– Вычитание, как и сложение, имеет свои свойства, – продолжил Электроша. – Если вы будете знать эти свойства и уметь ими пользоваться, то сможете правильно и быстро решать примеры.
– Электроша, а ты нам расскажешь о свойствах вычитания? – спросили мальчишки.
– Обязательно! – обрадовался Электроша. – Запомните! При вычитании число ноль обладает особым свойством. Если вычитаемое равно 0, то разность равна уменьшаемому. Справедливым является и такое свойство. Если уменьшаемое и вычитаемое равны, то разность равна 0.

– Давайте найдём, чему равна разность чисел 10 и 0 и чисел 20 и 20.
– В первом примере вычитаемое равно 0, значит, разность чисел равна уменьшаемому, то есть 10, – сказал Саша.
– А во втором примере уменьшаемое и вычитаемое равны, значит, их разность будет равна 0, – добавил Паша.

– Молодцы! – похвалил ребят Электроша. – А теперь давайте решим пример посложнее.
– Ну что здесь сложного, Электроша, – начал Саша. – В скобках записана сумма чисел 27 и 15, она равна…она равна 42. А потом от 127 отнимем 42 и получим…так, так, так…получим 85.
– Правильно, Саша! – сказал Электроша. – Но этот пример можно было решить иным способом, тогда решение стало бы гораздо проще. Смотрите, если бы сначала от числа 127 отняли 27. Эти же числа легче отнять, правда?
– Да, их разность равна 100, – сказал Саша.
– А потом от 100 отнимем 15 и получим 85. Это и есть одно из свойств вычитания.

Запомните! Правило вычитания суммы из числа: чтобы из числа вычесть сумму двух слагаемых, можно из этого числа вычесть одно из слагаемых и потом из результата вычесть другое слагаемое. В буквенном виде это свойство записывают так: a – (b + c) = a – b – c.

– А теперь давайте решим такой пример: найдём разность суммы чисел 19 и 5 и числа 9.
– Это легкотня! – начал Паша. – В скобках у нас записана сумма чисел 19 и 5. Она равна 24. Потом от 24 отнимем 9 и получим 15.
– Всё верно! – сказал Электроша. – Но, опять же, этот пример можно было решить проще. Смотрите, если бы мы сначала от 19 отняли 9, получили бы 10. А потом к 10 прибавили 5 и получили бы 15. Решить пример таким образом нам помогает очередное свойство вычитания.

Запомните! Правило вычитания числа из суммы: чтобы из суммы двух слагаемых вычесть число, можно вычесть это число из одного из слагаемых (если это слагаемое больше или равно вычитаемому) и потом к результату прибавить другое слагаемое. В буквенном виде это свойство записывают так: (a + b) – c = a – c + b.

– Ну а теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание, – предложил Электроша.
Итак, на отрезке АD отмечены точки B и C так, как показано на рисунке. Причём длина отрезка АD = 47 см, длина отрезка АB – 17 см, длина отрезка BC – 20 см. Какова длина отрезка CD?
Решение: в условии нам даны длина всего отрезка АD и длины отрезков АB и BC. А мы знаем свойство отрезка: длина всего отрезка равна сумме длин отрезков его составляющих. Тогда длина отрезка CD равна разности длины всего отрезка и суммы длин отрезков АB и BC. Подставим их длины. Получим 47 – (17 + 20). Применим правило вычитания суммы из числа и от 47 отнимем 17. Получим 30. А затем из 30 вычтем 20. И получаем, что длина отрезка CD равна 10 см.


 Получите свидетельство
Получите свидетельство Вход
Вход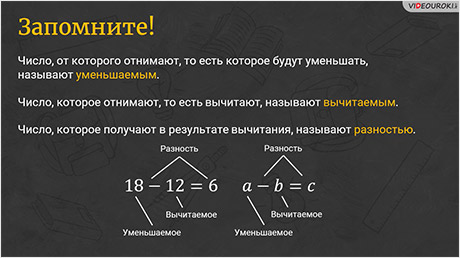



 3
3 3268
3268


Здравствуйте, Анжелика. Благодарим Вас за ценное замечание. Информация в уроке и в конспекте урока исправлена. Приносим наши искренние извинения! Если у Вас остались вопросы, напишите их, пожалуйста, в нашу службу техподдержки на email: [email protected]
Здравствуйте, Анжелика. Благодарим Вас за внимание к нашим проектам. Ваше замечание обязательно проверим.
Добрый вечер. Опечатка (математическая ошибка) в видео на 10:54 и опечатка в конспекте: