Представление чисел в компьютере. Вещественные числа

Вопросы занятия:

·        представление вещественных чисел в компьютере;

·        множество действительных чисел, представимых в памяти компьютера, дискретно, конечно и ограничено;

·        форматы представления вещественных чисел.

Как вы помните из курса математики, вещественные числа – это более широкий круг чисел, появление которых возникло из необходимости измерения несоизмеримых величин. Например, для извлечения корня, вычисления логарифмов, решения уравнений, исследования функций и прочее.

Данное множество включает в себя кроме целых чисел ещё и рациональные и иррациональные числа.

Понятие вещественного числа прошло долгий путь определения и становления. Ещё в Древней Греции в школе Пифагора было открыто существование несоизмеримых величин – несоизмеримость стороны и диагонали квадрата – то есть было открыто наличие иррациональных чисел.

Классическое определение вещественным числам дал в восемнадцатом веке Исаак Ньютон.

Понятно, что в математике множество вещественных чисел – бесконечно, непрерывно и не ограничено. Если представить числовую ось, то между двумя точками на числовой оси лежит бесконечное множество вещественных чисел.

Рассмотрим представление вещественных чисел в компьютере. Как вы помните, числа в компьютере представляются в двоичной системе счисления. Однако, в отличии от математики, множество вещественных чисел в компьютере – дискретно, ограничено и конечно. Опять же, как и в случае с целыми числами, из-за ограниченности размера ячейки памяти.

Рассмотрим пример.

Из математики известно, что дробь

 Здесь слово «бесконечная» означает, что в десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.

А слово «периодическая» означает, что это такая дробь, в которой бесконечно повторяется одна или несколько цифр. В нашем случае единица.

То есть обыкновенная дробь

Выполним деление на калькуляторе.

Итак, на табло калькулятора мы видим конечное число единиц после запятой.

Первый разряд отведён под знак числа. После запятой мы видим шестнадцать цифр, остальные не вместились в разрядную сетку. То есть мы получили не точное десятичное значение дроби одна девятая, а его сокращённое значение.

Следующее по величине число, которое может быть отображено на табло калькулятора будет больше предыдущего на величину, которая называется шагом числовой последовательности.

То есть можно сделать вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, потому что числа отделены друг от друга конечными отрезками.

Давайте узнаем будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел).

Вычислим выражение

То есть мы получили число, которое больше предыдущего числа в тысячу раз.  Как и в прошлый раз, наше число будет обрезанное.

Обратите внимание, шаг числовой последовательности изменится. Он, по сравнению с предыдущем примером, увеличится в тысячу раз.

То есть можно сделать вывод: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.

Отметим на числовой прямой точные значения вещественных чисел, которые можно представить на калькуляторе. Как видим, точки будут размещаться неравномерно: ближе к нулю – чаще, дальше от нуля – реже.

Все наши манипуляции с калькулятором также действительны и для компьютера, только с переходом на двоичную систему счисления и с учётом размера ячейки памяти компьютера.

В компьютере также, вещественные числа расположены неравномерно.

Множество вещественных чисел на калькуляторе и компьютере ограниченно и конечно из-за ограниченности разрядной сетки.

То есть самое большое число на разных калькуляторах будет различным. Так на самом простом калькуляторе, самое большое вещественное число будет 999999999. Если увеличить это число на единицу, то калькулятор выдаст сообщение об ошибке. На другом же калькуляторе, более усовершенствованном, самое большое число будет больше и если прибавить единицу, то вы получите следующий результат:

Для нас такая запись означает: единица, умноженная на десять в шестнадцатой степени.

Данный формат записи числа называют форматом с плавающей запятой, ранее мы рассматривали примеры только с фиксированной запятой.

Число, стоящее перед буквой е, называют мантиссой, число, стоящее после - порядком. Буква Е – это основание десятичной системы счисления.

То есть всякое вещественное число икс записывается в виде произведения мантиссы и основания системы счисления в некоторой целой степени, которую называют порядком:

Например, число 25324 можно представить различными способами

Рассмотрим представление 0,25324 • 10⁵

Здесь мантисса m = 0,25324, а n = 5 – порядок.

 Порядок указывает, на какое количество позиций и в каком направлении должна сместится десятичная запятая в мантиссе.

Мантисса числа для однозначности представления чисел с плавающей запятой должна иметь нормализованную форму, а именно представлять собой правильную дробь с цифрой после запятой, отличной от нуля;

Рассмотрим примеры нормализованного представления чисел.

Числа в компьютере могут представляться в формате как с фиксированной запятой, это, как правило, целые числа, так и в формате с плавающей запятой.

Но важно понимать, что и для числа, записанного в формате с плавающей запятой всегда есть ограничение – есть определённое самое большое число. Для нашего калькулятора это число

Положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю.

Эти числа являются целыми, но именно они ограничивают представление всех чисел: и целых, и вещественных, на калькуляторе.

Для компьютера эти ограничения конечно будут больше, но все равно будут. Как вы понимаете данное ограничение зависит от разрядности ячейки памяти и от того сколько разрядов выделяется под мантиссу и под порядок.

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. То есть наша ячейка в памяти может состоять из 32 или 64 клеточек. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Давайте разберёмся на примере. Возьмём число 125 в десятичной системе счисления и запишем её в 32-разрядную ячейку.

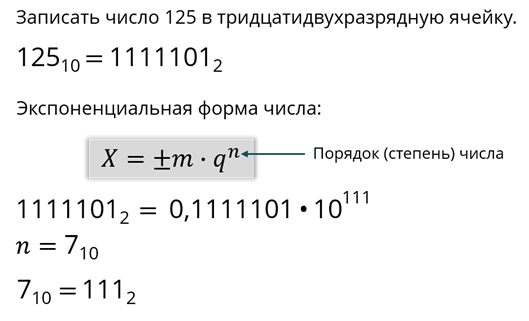
Мы записали двоичное число в экспоненциальной форме.

Теперь перенесём всё в клеточки ячейки памяти, размером 32 разряда.

Под знак и порядок выделяется 8 клеточек, под знак и мантиссу 24.

Первую клеточку слева выделяем под знак. Так как наше число положительное, то ставим цифру ноль. В разделе Знак и порядок запишем число семь в двоичной системе счисления. Оставшиеся клеточки заполним нулями.

Теперь переходим к разделу Знак и мантисса. В первой слева снова ставим цифру ноль, которая обозначает, что число положительное. Далее запишем наше число, а оставшиеся клеточки заполним нулями.

Мы записали наше число в тридцатидвухразрядную ячейку.

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка чисел, а точность – количеством разрядов, отведённых для хранения мантиссы.

Диапазон вещественных чисел ограничен, но он значительно шире, чем при представление целых чисел в форме с фиксированной запятой.

Например, при использовании 32-разрядной ячейки этот диапазон следующий:

Подводя итог нашего урока, можно сделать следующий вывод, что бесконечное, непрерывное и не ограниченное множество вещественных чисел в математике, в компьютерном представлении превращается в дискретное, ограниченное и конечное множество.

Итоги урока.

вещественные числа в компьютере представляются в формате с плавающей запятой.

всякое вещественное число X записывается в виде произведения мантиссы m и основания системы счисления q в некоторой целой степени n, которую называют порядком.

Нормализованной формой числа с плавающей запятой называется правильная дробь с цифрой после запятой, отличной от нуля.

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка чисел, а точность – количеством разрядов, отведённых для хранения мантиссы.