В прошлый раз мы с вами говорили об электрическом токе. Давайте вспомним, что под электрическим током понимают упорядоченное движение свободных носителей зарядов.
Также мы с вами выяснили, что основными характеристиками тока являются сила тока и напряжение. Силой тока мы с вами назвали скалярную физическую величину, численно равную электрическому заряду, протекающему через поперечное сечение проводника за единицу времени:

А напряжение — это скалярная физическая величина, равная работе электрического поля по перемещению единичного заряда из одной точки поля в другую:

Раз сила тока и напряжение характеризуют электрический ток и его действия, то между ними должна существовать какая-то зависимость. Вспомним её. Для этого проведём такой опыт. Возьмём резистор, который подключим в цепь с источником тока, выходное напряжение между клеммами которого можно регулировать. С помощью последовательно включённого амперметра и параллельно резистору вольтметра будем измерять силу тока и напряжение на спирали резистора.

Итак, начнём с напряжения в один вольт. Амперметр нам показывает силу тока 0,5 А. Увеличим напряжение в два раза. Сила тока в цепи возрастает до 1 А. Ещё в два раза увеличим напряжение — показания амперметра увеличиваются до 2 А. Таким образом получается, что во сколько раз мы увеличиваем напряжение на концах резистора, во столько же раз увеличивается и сила тока в нём.
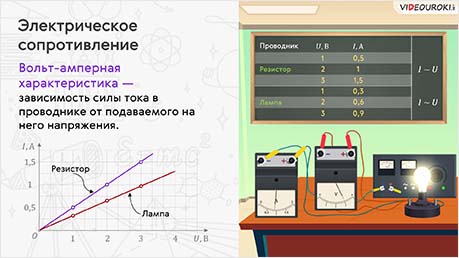
Если взять другой проводник, например лампу накаливания, и повторить с ней те же самые опыты, то мы увидим, что ток и в этом случае будет строго пропорционален напряжению на концах проводника.
Наблюдаемую зависимость силы тока в проводнике от напряжения можно изобразить графически. На таком графике в условно выбранном масштабе по оси абсцисс откладывается напряжение, а по оси ординат — сила тока.
Такой график в физике называют вольт-амперной характеристикой проводника.

А теперь, если по результатам проведённых опытов, определить отношение напряжения к силе тока для каждого из измерений то окажется, что оно постоянно для каждого из проводников, но имеет разное значение для разных проводников.

Следовательно, существует физическая величина, характеризующая свойства проводника, по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника или просто сопротивлением.
Давайте вспомним, что электрическое сопротивление — это скалярная физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока в нём.
А теперь проведём такой опыт. Соберём цепь, состоящую из источника постоянного тока, позволяющего регулировать выходное напряжение, магазина сопротивлений и амперметра. С помощью источника будем поддерживать в каждом случае постоянное напряжение, например, два вольта.
Будем поочерёдно включать в цепь проводники с различным сопротивлением
Для начала включим в цепь проводник сопротивлением один ом. Амперметр показывает нам силу тока два ампера. Теперь включим в цепь проводник, сопротивление которого два ома. Амперметр показывает ток, силой один ампер. Если же мы подключим в цепь проводник, сопротивлением четыре ома, то амперметр покажет ещё меньшую силу тока — всего пол ампера.

О чём нам говорят результаты эксперимента? Правильно, о том, что сила тока при постоянном напряжении на концах проводника обратно пропорциональна его сопротивлению:

Тогда, если обобщить результаты всех наших опытов, то можно утверждать, что сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению:

Эта зависимость была установлена экспериментально в 1826 году Георгом Омом. Поэтому данный закон называют законом Ома для участка цепи.
Закон Ома был, вероятно, самым важным из первых количественных описаний физики электричества. Сегодня нам кажется это почти очевидным. Но когда Ом впервые опубликовал свою работу, критики приняли её в штыки. А министр просвещения Германии вообще заявил, что «профессор, проповедующий такие ереси, недостоин преподавать науку».
Зная величину напряжения на концах проводника и ток в нём, по закону Ома можно вычислить сопротивление проводника, как отношение напряжения на концах проводника к силе тока в проводнике:

Из этой формулы можно вывести единицу сопротивления. Итак, за единицу сопротивления принимают сопротивление такого проводника, по которому проходит ток 1 А при напряжении на концах проводника 1 В. Эта единица сопротивления называется омом.


А теперь давайте вспомним, от чего зависит сопротивление конкретного проводника. Для этого проведём несколько простых опытов с панелью сопротивлений, представленной на экране. Итак, для начала включим в цепь источника тока половинку верхнего провода и измерим амперметром ток в цепи.
Теперь подключим весь провод. Как видно, ток в цепи стал слабее, причём почти в два раза. Значит, сопротивление проводника прямо пропорционально его длине.

Возьмём более толстую проволоку (в нашем случае — это два верхних провода, сложенных вместе). Мы видим, что сила тока увеличилась в два раза, по сравнению с прошлым показанием. Это приводит нас к выводу о том, что приводит нас к выводу о том, что сопротивление проводника обратно пропорционально площади его поперечного сечения.
Наконец подключим самую нижнюю проволоку, изготовленную из другого сплава, но длина и площадь сечения, которой такие же, что и у верхней проволоки. Легко заметить, что при одном и том же напряжении по нижнему проводнику идёт значительно меньший ток. Следовательно, проводники одинаковых размеров, но изготовленные из различных материалов, обладают неодинаковым сопротивлением.
Обобщив результаты наших опытов, мы можем утверждать, что: сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен:

Величина, обозначенная греческой буквой ρ, характеризует электрические свойства проводника. Она называется удельным сопротивлением. Это скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества, имеющего длину 1 м и площадь поперечного сечения 1 м2.
В СИ удельное сопротивление измеряется в Ом-метрах:

Но так как на практике длину проводников измеряют обычно в метрах, а площадь поперечного сечения в квадратных миллиметрах, то удельное сопротивление удобно записывать в виде «ом, умноженный на миллиметр квадратный, и делённый на метр»:

Например, у графита удельное сопротивление 13 Ом ∙ мм2/м. Значит, графитовый проводник длиной 1 м и поперечным сечением в 1 мм2 обладает сопротивлением 13 Ом. Будьте внимательны и всегда смотрите на единицу удельного сопротивления, когда пользуетесь табличными данными.
Значения удельного сопротивления веществ приведены для температуры двадцать градусов Цельсия, так как сопротивление проводников зависит от температуры: при повышении температуры удельное сопротивление возрастает, а при понижении уменьшается.
В заключение урока вспомним с вами о соблюдении общепринятой физической терминологии. Слово проводник у нас встречается часто в сочетании с тремя важнейшими электрическими величинами: силой тока, напряжением и сопротивлением. Все эти сочетания различны, поэтому будем писать и говорить:
сила тока в проводнике;
напряжение на проводнике;
и сопротивление проводника.

 Получите свидетельство
Получите свидетельство Вход
Вход




 1053
1053

