Действие магнитного поля на движущуюся заряженную частицу

На прошлых уроках мы с вами начали знакомство с магнитными полями. Давайте с вами вспомним, что магнитное поле — это особая форма материи, созданная движущимися (относительно определённой инерциальной системы отсчёта) электрическими зарядами или переменными электрическими полями.

Силовой характеристикой магнитного поля является вектор магнитной индукции, направление которого в данной точке совпадает с направлением силовой магнитной линии, проходящей через эту точку:

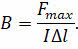
Так же мы с вами установили, что на проводник с током, помещённый в магнитное поле, со стороны магнитного поля действует сила, называемая силой Ампера. Её модуль равен произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока:

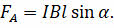
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих движущихся заряженных частиц. Следовательно, силу Ампера можно рассматривать как результат сложения сил, действующих на каждую движущуюся заряженную частицу.

Силу, с которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца.

Своё название сила получила в честь выдающегося голландского физика Хендрика Антона Лоренца — основателя электронной теории строения вещества.

Модуль силы Лоренца определяется отношением силы Ампера, действующей на участок проводника, находящийся в магнитном поле, к числу заряженных частиц, упорядоченно движущихся в этом участке проводника:

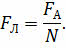
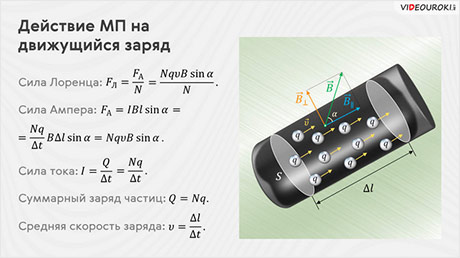
Давайте с вами рассмотрим прямолинейный участок проводника с током длиной Δl и площадью поперечного сечения S. При этом будем считать, что длина участка проводника и его площадь поперечного сечения настолько малы, что вектор магнитной индукции поля можно считать одинаковым в пределах этого участка проводника.

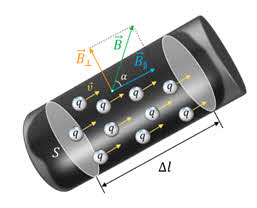
Итак, на участок проводника с током, находящимся в магнитном поле, действует сила Ампера, модуль которой равен произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока:

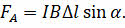
Теперь давайте с вами вспомним, что сила тока в проводнике определяется зарядом, прошедшим через поперечное сечение проводника за единицу времени:

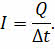
Здесь ∆t — это промежуток времени, за который заряженная частица проходит участок проводника длиной ∆l.

Пусть модуль заряда одной частицы равен q. Тогда суммарный заряд всех частиц равен произведению модуля заряда одной частицы на общее число частиц в выбранном участке проводника: Q = qN.

Перепишем уравнение для силы тока с учётом последнего равенства.

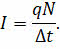
Полученное равенство подставим в закон Ампера:

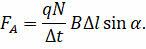
Обратите внимание на отношение ∆l/∆t — это есть не что иное, как модуль средней скорости заряженной частицы, упорядоченно движущейся в магнитном поле внутри проводника:

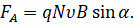
Теперь подставим полученное выражение для силы Ампера в формулу для силы Лоренца:

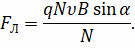
После упрощения получим, что модуль силы Лоренца равен произведению заряда частицы, модуля её средней скорости, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и вектором скоростью движения частицы:

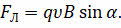
Направление силы Лоренца определяют по правилу левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости упорядоченного движения заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (или против движения отрицательного заряда), то отогнутый на 90^о большой палец укажет направление действующей на заряд силы Лоренца.

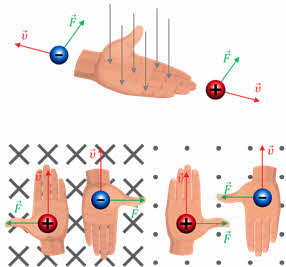
Анализ данного правила позволяет нам утверждать, что сила Лоренца, действующая на движущуюся в магнитном поле частицу, перпендикулярна вектору скорости этой частицы. Следовательно, сила Лоренца не совершает работы. Тогда, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль скорости частицы. А значит заряженная частица в магнитном поле движется с постоянной по модулю скоростью, но при этом направление скорости непрерывно изменяется.

Вид траектории заряженной частицы в магнитном поле зависит от угла между скоростью влетающей в поле частицы и магнитной индукцией. Рассмотрим такую ситуацию. Пусть протон, ускоренный разностью потенциалов U влетает в однородное магнитное поле сначала параллельно линиям индукции, затем — перпендикулярно, и, наконец, под некоторым углом к ним. Индукция магнитного поля равна B. Для каждого случая определите радиус кривизны траектории протона и период его обращения.

Итак, рассмотрим первый случай, когда протон, двигаясь по силовой линии в электрическом поле ускоренно, приобретает скорость, с которой влетает в однородное магнитное поле так, что его вектор скорости направлен вдоль поля (или противоположно направлению индукции магнитного поля).

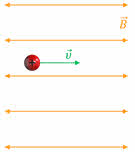
Очевидно, что в этом случае угол между направлением вектора скорости и индукции магнитного поля либо равен нулю, либо 180^о.

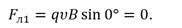
Тогда, согласно формуле, сила Лоренца, действующая на протон, равна нулю и частица будет продолжать двигаться равномерно прямолинейно.

Теперь рассмотрим второй случай, когда протон влетает в однородное магнитное поле перпендикулярно линиям его индукции.

В этом случае на протон в магнитном поле действует сила Лоренца, направленная перпендикулярно вектору скорости (направление силы Лоренца определяем по правилу левой руки). Как мы уже выяснили, сила Лоренца не может изменить модуль скорости заряженной частицы — она лишь меняет её направление. А так как магнитное поле однородно и вектор скорости частицы перпендикулярен линиям магнитной индукции, то протон под действием силы Лоренца начнёт двигаться по окружности.

С другой стороны, такое движение заряженной частицы в магнитном поле будет подчиняться второму закону Ньютона:

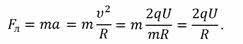
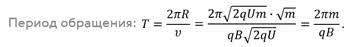
И нам осталось рассмотреть последний случай, когда частица влетает в магнитное поле под заданным углом к силовым линиям.

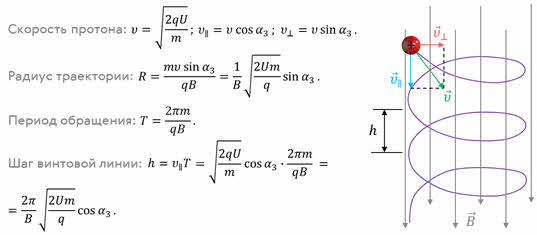
Подобное явление происходит в магнитном поле Земли. Движущиеся с огромными скоростями заряженные частицы из космоса «захватываются» магнитным полем Земли и образуют вокруг неё радиационные пояса. В них заряженные частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами. И только в полярных областях небольшая часть частиц вторгается в верхние слои атмосферы, вызывая восхитительные полярные сияния.

В заключении урока отметим, что действие магнитного поля на движущийся заряд широко используется в технике. Вспомните хотя бы электронно-лучевые трубки, применяемые в кинескопах телевизоров, где пучок летящих к экрану электронов отклоняется с помощью магнитных катушек.

Сила Лоренца используется и в циклотронах — особых ускорителях заряженных частиц. Обычный циклотрон состоит из двух полых полуцилиндров разного диаметра (дуантов), находящихся в однородном магнитном поле. Его принцип действия достаточно прост.

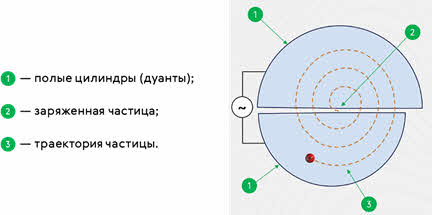
В зазоре между цилиндрами находится заряженная частица. В этом зазоре создаётся переменное электрическое поле с постоянным периодом, равным периоду обращения частицы. Это поле каждые пол периода разгоняет частицу, увеличивая при этом радиус её обращения (период обращения частицы не увеличивается). На последнем витке частица вылетает из циклотрона.

Действие силы Лоренца используют и в масс-спектрографах — устройствах, предназначенных для разделения частиц по их удельным зарядам, то есть по отношению заряда частицы к её массе, и по полученным результатам точно определять массы частиц. На экране вы видите схему простейшего масс-спектрографа. Цифрами один и два обозначены две диафрагмы, между которыми создаются взаимно перпендикулярные электрическое и магнитное поля. Заряженная частица, пройдя через первую диафрагму попадает в эти поля и, если сила Лоренца, действующая на неё, равна электростатической силе, то она сможет пройти через вторую диафрагму. Ионы же с другими скоростями отклонятся в полях и через вторую диафрагму не пройдут.

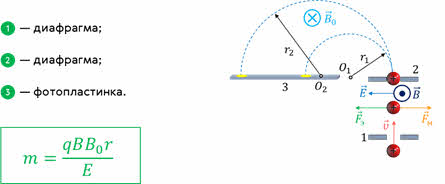
За диафрагмой создаётся постоянное магнитное поле, заставляющее заряженные частицы двигаться по окружности, радиус кривизны которой можно измерить, поставив на пути частиц фотопластинку. Так как скорость частиц одинакова и определяется постоянной прибора, то, зная заряд ионов, можно легко определить их массу.

Ещё одно устройство, в котором применяется действие силы Лоренца — это ТОКАМАК (тороидальная камера с магнитными катушками).

В нём плазма (напомним, что это частично или полностью ионизированный газ) удерживается в специально создаваемом сильном магнитном поле.  ТОКАМАК считается наиболее перспективным устройством для осуществления управляемого термоядерного синтеза.