Сегодня на уроке мы вспомним:
· Что такое модель и моделирование.
· Какие модели бывают.
· Этапы построения информационной модели.
· Классификацию информационных моделей.
· Рассмотрим способы решения задач по данной теме, которые могут быть на ОГЭ по информатике.
Одним из методов изучения каких-либо объектов окружающего мира является такой метод познания как моделирование.
Моделирование – это метод построения моделей, предназначенных для изучения и исследования объектов, процессов или явлений.
Модель – это искусственно созданный объект, который замещает исследуемый объект и отображает в более простом, уменьшенном виде структуру, свойства, взаимосвязи и отношения между его элементами.
Для каждой модели существует её прототип, или оригинал, – это исходный объект.
Модель не является точной копией объекта-оригинала.
Для того чтобы использовать ту или иную модель, необходимо, чтобы она имела все нужные свойства, отвечающие цели моделирования. Как мы помним, нельзя отразить все признаки объекта-оригинала в модели. В процессе моделирования выделяют главные, наиболее существенные, свойства объекта. Моделирование ставит целью понять сущность объекта, научиться им управлять, прогнозировать его состояние или действия. Моделируют как существующие предметы, явления, процессы, так и не существующие – это объекты, которые планируют разработать.
Вспомним способы отражения признаков оригинала в модели:
Копирование и воспроизведение признаков объекта-оригинала. Эта модель называется натурной, или материальной, – это уменьшенная или увеличенная копия, которая воспроизводит внешний вид объекта моделирования (манекен), его структуру (модель молекулы воды) или поведение (радиоуправляемая модель вертолёта).
Следующий способ – это описание признаков оригинала с помощью одного из языков кодирования информации. Здесь имеется ввиду словесное описание, формула, схема или чертёж. Такая модель называется информационной – это описание объекта-оригинала на одном из языков представления (кодирования) информации.
Любая модель создаётся для решения некоторой задачи. Вспомним этапы построения информационной модели.
Сначала необходимо проанализировать условие задачи, чтобы определить объект и цель моделирования. Затем нужно выделить в объекте моделирования свойства, основные части и связи между ними. То есть необходимо определить основные (существенные) данные: что дано, что необходимо найти, и указать связи между исходными данными и результатами.
Далее следует формализация. Это замена реального объекта его формальным описанием, то есть его информационной моделью. Здесь необходимо выразить связи и существенные признаки объекта в какой-либо форме (например, в виде словесного описания, таблицы, формулы и так далее).
Данные этапы выразим в виде схемы. На первом месте находится реальный объект. Затем в процессе анализа выделяются его существенные признаки. И далее в процессе формализации строится информационная модель.

Вспомним классификацию информационных моделей:
· По области использования. Это могут быть обучающие модели и тренажёры (используемые при обучении), игровые (например, репетиция поведения объекта в различных условиях), имитационные (это может быть отражение реальности в той или иной степени) и так далее.
· По фактору времени. По данному признаку выделяют следующие модели: статические и динамические. Статические модели описывают состояние системы в определённый момент времени. А динамические модели описывают процесс изменения и развития системы.
· По отрасли знаний. Это классификация по отрасли деятельности человека: математические, биологические, химические и так далее.
· По форме представлений. К таким видам информационных моделей относятся: образные модели, знаковые модели и смешанные модели.
К образным моделям относятся зрительные образы объектов, которые зафиксированы на каком-либо носителе. Например, рисунки в учебниках, фотографии, чертежи и так далее.
Знаковые модели представлены в виде текста, формул или программ на специальном языке программирования. К знаковым моделям относятся словесные описания, формулы в учебниках математики, физики и прочие.
Смешанные модели – это модели, в которых одновременно используются образные и знаковые модели. Смешанные модели включают в себя таблицы, графики, диаграммы и так далее.
Словесные модели – это описания предметов, явлений, событий, процессов на естественных языках. Как мы помним, естественный язык предназначен для общения людей.
Различают разговорный и книжный стили словесных описаний. Разговорный стиль, который происходит на естественном языке, обычно используется в общении для передачи своих мыслей, эмоций, чувств, то есть всего, что нас окружает.
Книжный стиль делят на следующие подкатегории:
· научный;
· официально-деловой;
· публицистический;
· художественный.
Основным языком информационного моделирования в науке является язык математики. Информационная модель, которая построена с использованием математических понятий и формул, называется математической моделью.
Математический язык состоит из разных формальных языков.
Вспомним требования к математическим моделям:
Универсальность. В модели должны быть полностью отображены все изучаемые свойства реального объекта.
Адекватность. Модель должна отображать все нужные свойства объекта с погрешностью не выше заданной.
Точность. Совпадение характеристик реального объекта и значений этих характеристик, полученных с помощью моделей, должны быть максимально точными.
Экономичность. Данное требование определяется затратами ресурсов ЭВМ (памяти и времени) на её реализацию и эксплуатацию.
С помощью алгебраического языка можно формализовать функциональные зависимости между количественными характеристиками объекта моделирования. Мы можем найти функциональные зависимости в школьном курсе физики. Это математические модели изучаемых процессов или явлений.
Если нужно построить логическую модель, то формализуются, то есть записываются в виде логических выражений, простые и сложные высказывания, которые выражены при помощи естественного языка.
Для выполнения математических моделей на компьютере могут использоваться:
· языки программирования,
· электронные таблицы,
· математические пакеты;
· программные средства для моделирования.
Компьютерные математические модели – это математические модели, реализованные на компьютере с помощью тех или иных программных средств для моделирования. С помощью специальных программ есть возможность исследовать объекты, которые опасно, дорого или невозможно исследовать напрямую; процессы, которые происходят очень быстро или медленно; явления, не происходящие раннее и так далее.
Имитационные модели – это модели систем, параметры которых могут принимать случайные значения в определённых пределах. Часто для того, чтобы оптимизировать работу такой системы, моделируют её работу при различных параметрах и находят их оптимальные значения.
Для решения некоторого задания на ОГЭ по информатике может понадобится применить алгоритм Дейкстры. Это алгоритм, который находит кратчайшее расстояние на графе от одной вершины до другой. Граф – это структура из точек-вершин, соединённых рёбрами-отрезками. Его можно представить как схему дорог или как компьютерную сеть. Рёбра – это связи, по ним можно двигаться от одной вершины к другой.
Алгоритм Дейкстры пошаговый. Сначала выбирается точка, от которой будут отсчитываться пути. Затем необходимо поочерёдно найти самые короткие маршруты из исходной точки в другие. Вершины, где уже побывали, отмечают посещёнными. Посещённые вершины используются, когда рассчитываются пути для не посещённых.
Решим задачу, которая может быть на ОГЭ по информатике, используя алгоритм Дейкстры.
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Для решения задачи воспользуемся алгоритмом Дейкстры.
Выписываем в отдельный список все возможные вершины графа.
Построим дерево. Нарисуем стартовую вершину (здесь это будет точка А) и подпишем рядом с ней расстояние, которое нужно «проехать», чтобы добраться до неё из стартовой точки А. То есть пишем ноль. Эта вершина будет корнем нашего дерева.
Найдём вершину с наименьшим числом, сейчас это только одна вершина – А.
Вычёркиваем её из списка доступных вершин. Далее эту вершину мы больше не будем рассматривать в качестве возможной вершины дерева. Таким образом вершины, которые вычёркиваются больше не дорисовываются. Так как расстояния от стартовой вершины до них уже подсчитаны и лучше уже не станут. Следующее действие делаем из вершины А.
Смотрим на таблицу расстояний. Находим вершины, до которых идёт ребро из текущей вершины и которые ещё не вычеркнуты. Это вершины В, С и D. Рисуем из текущей вершины А ветви дерева для каждой из найденных смежных вершин.
На ветвях подписываем длины рёбер по таблице расстояний.
Для полученных вершин посчитаем расстояние до них: расстояние до текущей вершины плюс расстояние (длина ребра) до каждой полученной вершины. Записываем полученные расстояния возле каждой вершины.
Теперь находим вершину с наименьшим расстоянием. Сейчас это вершина D. Вычёркиваем её из списка доступных вершин. Далее действия выполняем из неё.
Находим по таблице расстояний все вершины, до которых идёт ребро из текущей вершины D и которые ещё не вычеркнуты. Это вершины B и C.
Рисуем из вершины D ветви дерева для вершин B и C. Подписываем длины рёбер.
Для каждой полученной вершины посчитаем расстояние до неё, как делали ранее. Записываем эти расстояния рядом с каждой вершиной.
Теперь ищем одинаковые вершины.
На данный момент это пара вершин B3 и B4 и пара C6 и C5. Для каждой пары одинаковых вершин вычёркиваем ту вершину, которая имеет большее расстояние до неё.
Как видим, сейчас это вершины B4 и C6.
Если пары одинаковых вершин имеют равные расстояния, то вычёркиваем одну любую.
Идём дальше. Находим вершину с наименьшим расстоянием. Сейчас это вершина B. Вычёркиваем её из списка доступных вершин.
По таблице расстояний ищем все вершины, до которых идёт ребро из текущей вершины B и которые ещё не вычеркнуты. Это вершина C. Рисуем из вершины B ветвь дерева для вершины C. Подписываем длину ребра.
Для полученной вершины посчитаем расстояние до неё. Записываем это расстояние рядом с вершиной.
Снова находим одинаковые вершины – это C4 и C5. Вычёркиваем вершину C5, так как она имеет бoльшее расстояние до неё.
Продолжаем. Находим вершину с наименьшим расстоянием. Сейчас это вершина Цэ. Вычёркиваем её из списка доступных вершин.
По таблице расстояний видим, что вершина Е – это вершина, до которой идёт ребро из текущей вершины C и которая ещё не вычеркнута. Рисуем из вершины C ветвь дерева для вершины Е. Подписываем длину рёбра.
Для полученной вершины посчитаем расстояние до неё. Записываем это расстояние рядом с вершиной.
Находим одинаковые вершины. Сейчас таких пар нет. Находим вершину с наименьшим расстоянием. В данном случае это вершина Е. Вычёркиваем её из вписка доступных вершин. Как видим, это последняя вершина, расстояние до которой мы искали. Алгоритм закончен.

Ответ: 7 километров.
Решим ещё одну задачу. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

Определите длину кратчайшего пути между пунктами А и E, проходящего через пункт D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
В этот раз задачу решим немного другим способом. Если внимательно посмотреть, то мы увидим, что таблица симметрична, поэтому смело работаем далее только с одной стороной.
Рассмотрим с какими пунктами пересекается пункт А и какое расстояние между ними.
У пункта А есть пересечение с пунктом B.
Ставим в произвольном месте точки А и B. Соединяем их и подписываем расстояние.
Также А пересекается с пунктом C. Ставим точку C и соединяем её с точкой А, не забываем подписать расстояние. Ставьте точки так, чтобы линии не пересекались.
Таким же образом добавляем точки D и Е, так как пункт А пересекается с пунктами D и Е. Подписываем расстояния между ними.
С пунктом А закончили. Теперь рассматриваем пункт B. У него пересечение только с пунктом D. Соединяем точки B и D и подписываем расстояние.
Пункт C пересекается с пунктами Дэ и Е. Соединяем точки, подписываем расстояния.
Пункт D пересекается только с пунктом Е. Также соединяем нужные точки и подписываем расстояния.
Обратите внимание, что линии не обязаны быть прямыми, поэтому чтобы они не пересекались их можно рисовать, например, в виде дуги.
Итак, мы отобразили все сведения из таблицы.
Нам необходимо определить длину кратчайшего пути между пунктами А и E, проходящего через пункт D.
Разберём несколько вариантов маршрутов.
Теперь подставим значения и посчитаем длину каждого маршрута.
Как видим, кратчайшее расстояние от пункта А до пункта Е, с обязательным посещением пункта Дэ, равно 10 километров.

В конце урока попробуйте ответить на следующие вопросы:
Что такое моделирование?
Как называется описание объекта-оригинала на одном из языков представления (кодирования) информации?
Что такое формализация?
Правда ли, что моделировать можно как существующие предметы, явления, процессы, так и не существующие – это объекты, которые планируют разработать, явления, которые могут пройти или нет?
Внимательно посмотрев урок, вам не составит труда ответить на вопросы.

 Получите свидетельство
Получите свидетельство Вход
Вход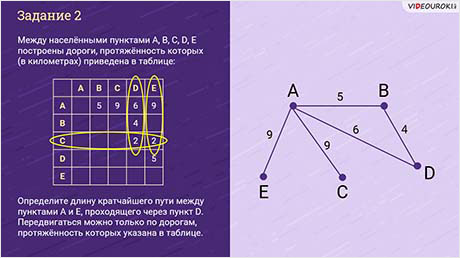




 4507
4507

