Сегодня на уроке мы с вами вспомним, как устанавливается соответствие между действительными точками и точками окружности с помощью поворота точки окружности, а также вспомним, что называют синусом, косинусом и тангенсом произвольного угла. Скажем, какие функции называются тригонометрическими функциями. Выясним, что является областью определения и множеством значений тригонометрических функций.
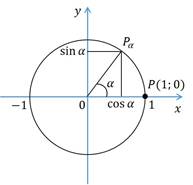
Прежде чем приступить к рассмотрению новой темы, давайте возьмём окружность
единичного радиуса с центром в начале координат и отметим на ней точку 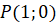 .
.
Тогда при повороте точки 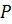 на угол
на угол 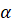 радиан мы получим точку
радиан мы получим точку 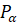 . При этом помним, что ордината точки
. При этом помним, что ордината точки 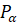 – это синус угла
– это синус угла 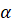 , а абсцисса этой точки – это косинус угла
, а абсцисса этой точки – это косинус угла 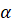 .
.
Далее считаем, что все углы измерены в радианной мере, и поэтому обозначение «радиан», как правило, опускается. Договорившись считать единицу измерения углов (1 радиан) фиксированной, определяем, например, синус числа x как синус угла в x радиан; косинус числа x как косинус угла в x радиан и так далее.
Так, каждому действительному числу x поставлены в соответствие
числа синус x и косинус x, то есть на множестве действительных чисел определены функции 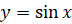 и
и 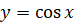 .
.
Получается, что областью определения функций игрек 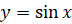 и
и 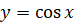 является множество
является множество 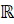 всех действительных чисел.
всех действительных чисел.
Давайте найдём множество значений функции 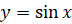 . Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых
. Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых 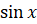 равен y.
равен y.
Мы знаем, что уравнение 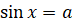 имеет корни, если
имеет корни, если 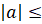 . И уравнение не имеет корней, если
. И уравнение не имеет корней, если 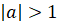 . Из этого следует, что множеством значений функции
. Из этого следует, что множеством значений функции 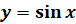 является отрезок
является отрезок 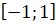 .
.
Найдём множество значений функции 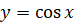 . Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых
. Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых 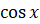 равен y.
равен y.
Знаем, что уравнение 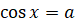 имеет корни, если
имеет корни, если 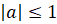 . И уравнение не имеет корней, если
. И уравнение не имеет корней, если 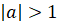 .
.
А значит, множеством значений функции 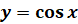 является отрезок
является отрезок 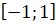 .
.
Таким образом, можно сказать, что функции 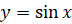 и
и 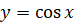 являются ограниченными.
являются ограниченными.
Теперь поговорим про функцию 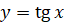 . Она определяется формулой
. Она определяется формулой 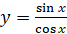 .
.
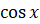 не должен обращаться в нуль, так как делить на нуль нельзя.
не должен обращаться в нуль, так как делить на нуль нельзя.
Функция 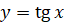 определена при тех значениях x, для которых
определена при тех значениях x, для которых 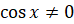 .
.
Мы знаем, что решением уравнения 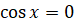 является
является 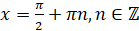 .
.
Тогда областью определения функции 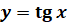 является множество
является множество 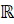 всех действительных чисел, кроме
всех действительных чисел, кроме 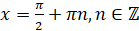 .
.
Известно, что уравнение 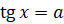 имеет корни при любом действительном значении
имеет корни при любом действительном значении 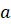 . Следовательно, множеством значений функции
. Следовательно, множеством значений функции 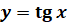 является множество
является множество 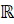 всех действительных чисел.
всех действительных чисел.
Осталось выяснить, что является областью определения и множеством
значений функции 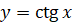 . Запишем:
. Запишем: 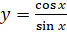 . Здесь
. Здесь 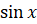 не должен обращаться в нуль, так как делить на нуль нельзя. А
значит, функция
не должен обращаться в нуль, так как делить на нуль нельзя. А
значит, функция 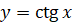 определена при тех значениях x, для которых
определена при тех значениях x, для которых 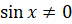 .
.
Корнем уравнения 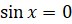 является
является 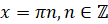 . Тогда областью определения функции
. Тогда областью определения функции 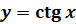 является множество
является множество 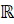 всех действительных чисел, кроме
всех действительных чисел, кроме 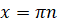 ,
, 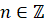 .
.
Уравнение 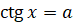 имеет корни при любом действительном значении a, а значит, множеством
значений функции
имеет корни при любом действительном значении a, а значит, множеством
значений функции 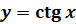 является множество
является множество 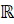 всех действительных чисел.
всех действительных чисел.
Таким образом, мы с вами выяснили, что является областью
определения и множеством значений функций 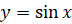 ,
, 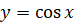 ,
, 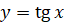 и
и 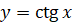 . Эти функции называются тригонометрическими функциями.
. Эти функции называются тригонометрическими функциями.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите область определения функций:
а) 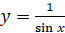 ; б)
; б) 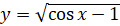 ; в)
; в) 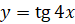 .
.
Решение.


Задание второе. Найдите множество значений функций:
а) 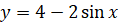 ; б)
; б) 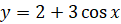 .
.
Решение.


Задание третье. Найдите наибольшее и наименьшее значения функции
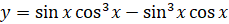 .
.
Решение.
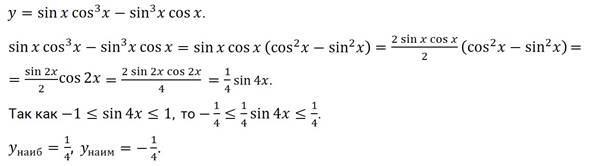

 Получите свидетельство
Получите свидетельство Вход
Вход




 1
1 10273
10273



Здравствуйте. А есть ли в комплекте текстовые документы с текстами уроков?