Тест на повторение_ЕГЭ 1-10

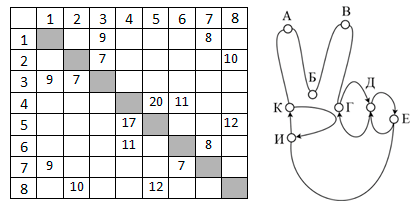
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице приведены длины дорог между пунктами. 

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего кольцевого маршрута, проходящего через все пункты и оканчивающемся в пункте, из которого было начато движение. Передвигаться можно только по указанным дорогам. В ответе запишите целое число – длину пути в километрах.

Логическая функция F задаётся выражением x ∧ (y → z) ∨ w. Ниже приведён частично заполненный фрагмент таблицы истинности этой функции, содержащий неповторяющиеся строки. Сколькими способами можно поставить в соответствие переменные w, x, y, z столбцам таблицы истинности функции F, опираясь на информацию из данного фрагмента?

Пример. Функция F задана выражением x ∨ y ∨ z, а фрагмент таблицы истинности имеет вид:

В этом случае переменные можно расставить любым способом, значит, ответом будет число 6.

В файле 3-40.xls приведён фрагмент базы фрагмент базы данных «Города и страны», описывающей различные страны, города и языки. База данных состоит из трех таблиц. Таблица «Страны» (код, название, континент, регион, площадь, год получения независимости, население, ОПЖ – ожидаемая продолжительность жизни, ВНД – валовый национальный доход, предыдущее значение ВНД, форма правления, идентификатор столицы). Таблица «Города» (идентификатор, название, код страны, район, население). Таблица «Языки» (код языка, код страны, название, является ли официальным, процент использования в стране). По некоторым значениям данных нет, в этом случае в таблице внесено значение NULL. На рисунке приведена схема базы данных.

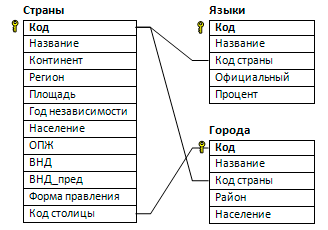
Используя информацию из приведённой базы данных, определите среднее население стран Европы, в которых наиболее популярный официальный язык используют менее 60% населения. В ответе укажите только целую часть получившегося числа.

По каналу связи передаются сообщения, содержащие только шесть букв: О, Т, П, У, С, К. Для передачи используется двоичный код, удовлетворяющий условию Фано. Укажите минимальную возможную длину закодированной последовательности КУСОККОПУСТ, если известно, что код для С – 01.

Автомат обрабатывает натуральное число N<256 по следующему алгоритму:

1) Строится восьмибитная двоичная запись числа N.
2) Инвертируются все разряды исходного числа (0 заменяется на 1, 1 на 0).
3) К полученному двоичному числу прибавляют единицу.
4) Полученное число переводится в десятичную систему счисления.

Для какого числа N результат работы алгоритма равен 221?

 Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 2 команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 7 
[ Вперед 20 Направо 240 Вперед 10 Направо 240 
  Вперед 20 Направо 120 Вперед 10 Направо 120]

Сколько точек с целочисленными координатами расположены внутри замкнутых областей?

Каким может быть максимальное количество цветов в палитре, чтобы растровое изображение размером 5524х8595 пикселей можно было сохранить, используя 52 Мбайт памяти? В ответе запишите только целое число, единицу измерения писать не нужно.

Петя составляет список из 4-буквенных слов, в состав которых входят только буквы О, С, Е, Н, Ь. Петя расположил слова в обратном алфавитном порядке. Вот начало списка:

1. ЬЬЬЬ
2. ЬЬЬС
3. ЬЬЬО
4. ЬЬЬН
5. ЬЬЬЕ
6. ЬЬСЬ
...

Запишите слово, которое стоит в этом списке под номером 100.

Откройте файл электронной таблицы 9-127.xls, содержащей в каждой строке три натуральных числа, являющиеся коэффициентами (a,b,c) квадратного уравнения a·x²+b·x+c=0. Выясните, какое количество уравнений имеют два действительных корня.

В файле 10-141.docx приведена книга Н.В. Гоголя «Вечера на хуторе близ Диканьки». Сколько раз слово «сабля» (во всех формах единственного и множественного числа) встречается в тексте повести «Страшная месть» (не считая сносок)? Регистр написания слова не имеет значения. В ответе укажите только число.