Проверочный тест по темам ЕГЭ - 1, 13 (2 вариант)
Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице числами обозначены длины дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
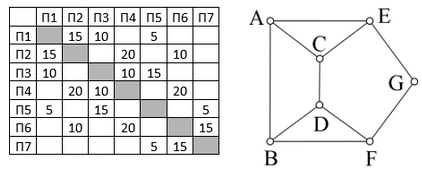 Найдите номера пунктов в таблице, соответствующие пунктам А и В на схеме, если известно, что дорога между А и В длиной 10 километров. В качестве ответа запишите без разделителей два числа – номера пунктов в таблице, соответствующие пунктам А и В на схеме, в порядке возрастания.
Найдите номера пунктов в таблице, соответствующие пунктам А и В на схеме, если известно, что дорога между А и В длиной 10 километров. В качестве ответа запишите без разделителей два числа – номера пунктов в таблице, соответствующие пунктам А и В на схеме, в порядке возрастания.
Вопрос 2
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
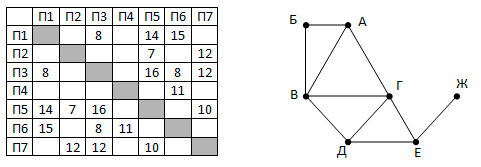 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Укажите кратчайший путь из пункта Б в пункт Ж. В ответе перечислите все населённые пункты, через которые проходит путь. Например, путь из Г в В через А и Б записывается как ГАБВ.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Укажите кратчайший путь из пункта Б в пункт Ж. В ответе перечислите все населённые пункты, через которые проходит путь. Например, путь из Г в В через А и Б записывается как ГАБВ.
Вопрос 3
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта А в пункт Д.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта А в пункт Д.
Вопрос 4
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город К? Длиной пути считать количество дорог, составляющих этот путь.
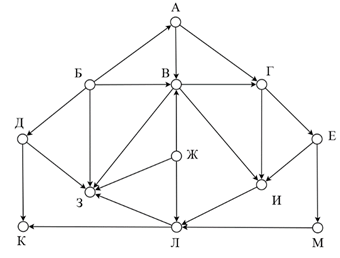
Вопрос 5
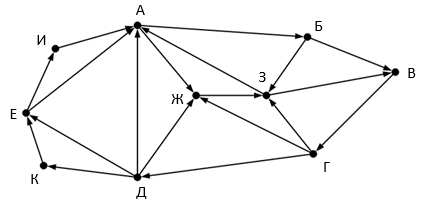
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует маршрутов из А в З, проходящих через город Е?
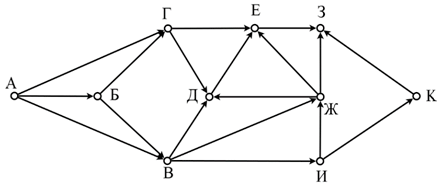
Вопрос 6
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе З, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Получите комплекты видеоуроков + онлайн версии
 0
0 298
298 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








