ЕГЭ тест №24 (Вариант № 56162)
Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
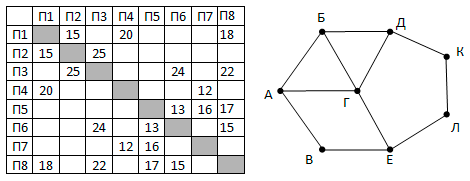
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта Е в пункт Л.
Вопрос 2
Логическая функция F задаётся выражением (a → b) ∧ ¬(b ≡ c) ∧ (d → a). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Вопрос 3
В файле 3-40.xls приведён фрагмент базы фрагмент базы данных «Города и страны», описывающей различные страны, города и языки. База данных состоит из трех таблиц. Таблица «Страны» (код, название, континент, регион, площадь, год получения независимости, население, ОПЖ – ожидаемая продолжительность жизни, ВНД – валовый национальный доход, предыдущее значение ВНД, форма правления, идентификатор столицы). Таблица «Города» (идентификатор, название, код страны, район, население). Таблица «Языки» (код языка, код страны, название, является ли официальным, процент использования в стране). По некоторым значениям данных нет, в этом случае в таблице внесено значение NULL. На рисунке приведена схема базы данных.
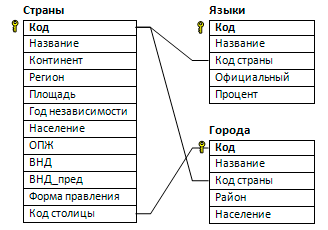
Используя информацию из приведённой базы данных, определите среднее население стран Европы, в которых наиболее популярный официальный язык используют менее 60% населения. В ответе укажите только целую часть получившегося числа.
Вопрос 4
По каналу связи передаются сообщения, содержащие только 4 буквы: Л, Е,Т, О; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, Л используются такие кодовые слова:
Т – 101, О – 01, Л – 11.
Укажите такое кодовое слово для буквы Е, при котором код будет допускать однозначное декодирование, при этом его длина должна быть наименьшей.
Вопрос 5
Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1) Строится двоичная запись числа N.
2) Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3) Шаг 2 повторяется ещё два раза.
4) Результат переводится в десятичную систему счисления.
При каком наибольшем исходном числе N < 80 в результате работы алгоритма получится чётное число, которое не делится на 4?
Вопрос 6
Определите, при каком наименьшем введённом значении переменной s программа выведет число 10.
s = int(input())
n = 0
while s < 1000:
s = s * 2
n = n + 5
print(n)
Вопрос 7
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 80 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза ниже и частотой дискретизации в 1,5 раз выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 3 раза ниже, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?
Вопрос 8
Миша составляет 6-буквенные коды из букв Б, А, Н, К, И, Р. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Миша?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите количество дней в июне, когда температура в 21:00 была выше, чем средняя температура в этот день.
Вопрос 10
В файле 10-170.docx приведена повесть-феерия А. Грина «Алые паруса». Сколько раз встречается слово «что» (с заглавной или строчной буквы) в тексте повести (не считая сносок)? В ответе укажите только число.
Вопрос 11
В некоторой стране автомобильный номер длиной 7 символов составляется из заглавных букв (всего используется 22 буквы) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 50 автомобильных номеров.
Вопрос 12
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 247 идущих подряд цифр 5? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (555)
ЕСЛИ нашлось (222)
ТО заменить (222, 5)
ИНАЧЕ заменить (555, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Вопрос 13
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Н и проходящих через пункт Г или через пункт Е, но не через оба этих пункта?
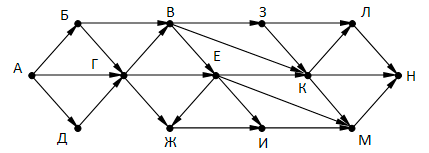
Вопрос 14
Значение арифметического выражения: 3260 + 4180 – 128 записали в системе счисления с основанием 8. Сколько цифр «7» в этой записи?
Вопрос 15
Укажите наименьшее целое значение А, при котором выражение
( – 2y + 3x < A) ∨ (x > 20) ∨ (y > 55)
истинно для любых целых положительных значений x и y.
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 + 2·n при n < 5 F(n) = 2·(n + 1)·F(n–2), если n ≥ 5 и делится на 3, F(n) = 2·n + 1 + F(n–1) + 2·F(n–2), если n ≥ 5 и не делится на 3.
Чему равно значение функции F(15)?
Вопрос 17
В файле 17-4.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 10 000 включительно. Определите количество пар, в которых хотя бы один из двух элементов больше, чем среднее арифметическое всех чисел в файле, а их сумма оканчивается на 9. В ответе запишите два числа: сначала количество найденных пар, а затем – минимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 2. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 3. Укажите минимальное значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 21
Укажите наименьшее трехзначное натуральное число, при вводе которого приведенная ниже программа напечатает число 0.
n = int(input())
i = 0
while n > 0:
i = i + n % 20
n = n // 20
printf(i % 19)
Вопрос 22
У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1 2. увеличь число десятков на 1
Например: при помощи команды 2 число 23 преобразуется в 33. Если перед выполнением команды 2 вторая с конца цифра равна 9, она не изменяется.
Сколько есть программ, которые число 12 преобразуют в число 36?
Получите комплекты видеоуроков + онлайн версии
 0
0 1124
1124 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








