ЕГЭ тест №22 (Вариант № 10547)

Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
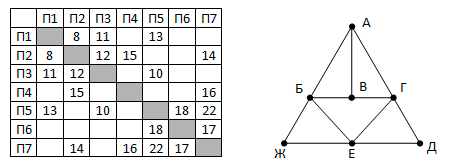
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина кратчайшего пути из пункта A в пункт Ж превышает 30 километров. Определите длину кратчайшего пути между пунктами В и Е.
Вопрос 2
Логическая функция F задаётся выражением (a ∧ ¬c) ∨ (¬a ∧ b ∧ c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
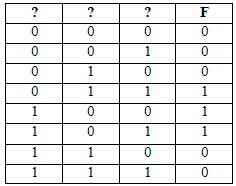
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Вопрос 3
В файле 3-5.xls приведён фрагмент базы фрагмент базы данных «Аудиотека». База данных состоит из четырёх таблиц. Таблица «Альбомы» содержит записи о записанных альбомах, а также информацию о исполнителях. Таблица «Артисты» содержит записи о названии исполнителей. Таблица «Треки» содержит записи о записанных композициях, а также информацию о альбомах и жанрах. Поле Длительность содержит длительность аудиозаписи в миллисекундах, поле Размер содержит размер аудиозаписи в байтах, а поле Стоимость содержит стоимость аудиозаписи в рублях. Таблица «Жанры» содержит данные о названии жанров. На рисунке приведена схема указанной базы данных.
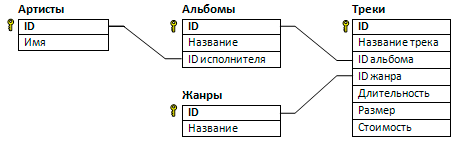 Используя информацию из приведённой базы данных, найдите исполнителя в жанре Rock с наименьшей суммарной длительностью песен в этом жанре. В ответе укажите целую часть длительности его песен в секундах.
Используя информацию из приведённой базы данных, найдите исполнителя в жанре Rock с наименьшей суммарной длительностью песен в этом жанре. В ответе укажите целую часть длительности его песен в секундах.
Вопрос 4
По каналу связи передаются сообщения, содержащие только восемь букв: Г, Д, Е, С, О, Т, К, А; для передачи используется двоичный код, удовлетворяющий условию Фано. Буквы С, Е, К, Т, А имеют коды 111, 110, 10, 0010, 0011 соответственно. Укажите наименьшую возможную длину закодированной последовательности для слова КОКОСЕГ.
Вопрос 5
Автомат обрабатывает натуральное число N < 256 по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Инвертируются все разряды исходного числа, кроме последней единицы и стоящих за ней нулей (0 заменяется на 1, 1 на 0).
3) Полученное число переводится в десятичную систему счисления.
Для какого значения N результат работы алгоритма равен 6?
Вопрос 6
Определите, при каком наибольшем положительном введённом значении переменной s программа выведет трёхзначное число.
s = int(input())
n = 200
while s // n >= 2:
s = s + 5
n = n + 5
print(s)
Вопрос 7
Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 224 = 16 777 216 цветов. Средний размер фотографии составляет 15 Мбайт. Для хранения в базе данных фотографии преобразуют в формат с палитрой, содержащей 256 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?
Вопрос 8
Петя составляет 7-буквенные слова из букв А, Б, Р, И, К, О, С. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Петя?
Вопрос 9
Откройте файл электронной таблицы 9-127.xls, содержащей в каждой строке три натуральных числа, являющиеся коэффициентами (a,b,c) квадратного уравнения a·x2+b·x+c=0. Коэффициенты a, b и с записаны соответственно в столбцах A, B и C электронной таблицы. Выясните, какое количество уравнений имеют два равных действительных корня (один кратный корень).
Вопрос 10
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «день» или «День» в тексте романа в стихах А.С. Пушкина «Евгений Онегин» (файл 10-0.docx). Другие формы слова «день», такие как «дни», «днями» и т.д., учитывать не следует. В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из набора И,Н,Ф, О, Р, М, А, Т, К. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти в байтах, отводимый этой программой для записи 25 паролей.
Вопрос 12
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (555) ИЛИ нашлось (333)
ЕСЛИ нашлось (555)
ТО заменить (555, 3)
ИНАЧЕ заменить (333, 5)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Дана строка, состоящая из 300 цифр 5. Сколько пятёрок останется в строке после обработки по этой программе?
Вопрос 13
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, С, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Т?
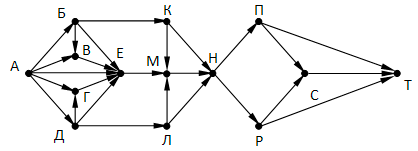
Вопрос 14
Сколько единиц в двоичной записи числа 42015 + 22015 – 15?
Вопрос 15
Укажите наименьшее целое значение А, при котором выражение
(y + 3x < A) ∨ (x > 9) ∨ (y > 20)
истинно для любых целых положительных значений x и y.
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1 F(n) = F(n–1), при 0 < n ≤ 10 F(n) = 2,2*F(n–3), при 10 < n < 100 F(n) = 1,7*F(n–2), при n ≥ 100
Чему равно значение функции F(22)? В ответе запишите только целое число.
Вопрос 17
В файле 17-3.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых чётность чисел различна, при этом чётное число делится на 4, а нечётное на 11, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч два камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 55 или больше камней.
В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 45. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч два камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 55 или больше камней.
В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 45. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 2. Укажите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч два камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 55 или больше камней.
В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 45. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 3. Найдите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Найденные значения запишите в ответе в порядке возрастания.
Вопрос 21
Получив на вход число x, этот алгоритм печатает два числа a и b. Сколько существует таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 0?
x = int(input())
a = 0; b = 1
while x > 0:
a = a + 1
b = b*(x%10)
x = x//10
print(a, b)
Вопрос 22
У исполнителя Калькулятор есть три команды, которым присвоены номера:
1. Прибавить 1 2. Прибавить 2 3. Умножить на 2
Сколько разных чисел на отрезке [34, 59] может быть получено из числа 1 с помощью программ, состоящих из 6 команд?
Получите комплекты видеоуроков + онлайн версии
 0
0 950
950 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








