ЕГЭ тест №20 (Вариант № 10755)
Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
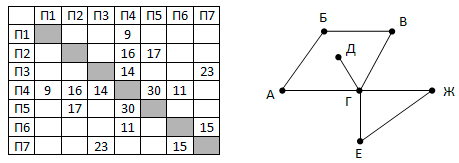
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта Е в пункт Ж.
Вопрос 2
Логическая функция F задаётся выражением (x ≡ ¬z) → ((x ∨ w) ≡ y).
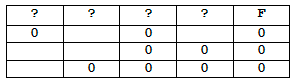
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-30.xls приведён фрагмент базы фрагмент базы данных «Русский рок», описывающей советские и российские рок-группы. База данных состоит из двух таблиц. Таблица «Группы» содержит информацию о музыкальных коллективах: ID, название, год основания. Таблица «Альбомы» содержит информацию о студийных музыкальных альбомах: ID, название, ID группы, год издания, количество песен. Для каждой группы в базе данных указано ровно 3 альбома. На рисунке приведена схема базы данных.
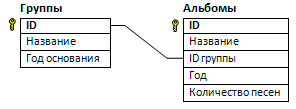
Используя информацию из приведённой базы данных, определите, у скольких групп из указанных в базе данных с момента основания и до выхода первого из указанных альбомов прошло не более 5 лет.
Вопрос 4
Для кодирования некоторой последовательности, состоящей из букв П, О, Е, Х, А, Л, И, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110, 1010, 001. Найдите наименьшую возможную суммарную длину всех кодовых слов.
Вопрос 5
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Какое минимальное число R, большее 144, может быть получено в результате работы автомата?
Вопрос 6
При каком наибольшем введенном числе d после выполнения программы будет напечатано 150?
d = int(input())
n = 3
s = 38
while s <= 1200:
s = s + d
n = n + 7
print(n)
Вопрос 7
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 96 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза выше и частотой дискретизации в 3 раза ниже, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 16 секунд. Во сколько раз пропускная способность канала в город Б больше пропускной способности канала в город А?
Вопрос 8
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные. Сколько различных кодов может составить Артур?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите количество дней, когда средняя температура с 07:00 до 10:00 (включительно) была ниже, чем средняя температура с 19:00 до 22:00 (включительно).
Вопрос 10
В файле 10-141.docx приведена книга Н.В. Гоголя «Вечера на хуторе близ Диканьки». Сколько раз слово «есаул» (во всех формах единственного числа) встречается в тексте повести «Страшная месть» (не считая сносок)? Регистр написания слова не имеет значения. В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы И, К, Л, М, Н. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти в байтах, отводимый этой программой для записи 20 паролей.
Вопрос 12
Дана программа для исполнителя Редактор:
ПОКА нашлось(43) ИЛИ нашлось(53)
ЕСЛИ нашлось(43)
ТО заменить(43, 33)
ИНАЧЕ заменить(53, 433)
КОНЕЦ ПОКА
Определите максимально возможное количество цифр 3, которое может получиться в результате применения этой программы к строке, состоящей из 17 цифр 3, 23 цифр 4 и 29 цифр 5, идущих в произвольном порядке.
Вопрос 13
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и НЕ проходящих через город Г?
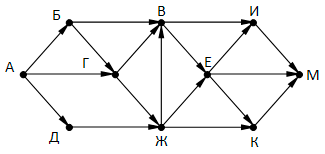
Вопрос 14
Значение выражения 7103 – 6∙770 + 3∙757 – 98 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Вопрос 15
Элементами множеств А, P, Q являются натуральные числа, причём P={2,4,6,8,10,12} и Q={4,8,12,116}. Известно, что выражение
(x ∈ P) → (((x ∈ Q) ∧ (x ∉ A)) → (x ∉ P))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = 1, при n < 2, F(n) = F(n/2) + 1, когда n ≥ 2 и чётное, F(n) = F(n - 3) + 3, когда n ≥ 2 и нечётное.
Назовите минимальное значение n, для которого F(n) равно 31.
Вопрос 17
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит одна куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) убрать из кучи половину камней, если количество камней в куче делится на 2; иначе убрать из кучи два камня;
б) убрать из кучи две трети камней, если количество камней в куче делится на 3; иначе убрать из кучи три камня.
Например, пусть в куче 10 камней, тогда можно убрать половину или только три камня. А если в куче 12 камней, то можно убрать половину или две трети камней. Игра завершается в тот момент, когда в куче останется ровно 1 камень. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет ровно 1 камень. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 1. Найдите максимальное значение S, при котором Ваня может выиграть своим первым ходом после неудачного хода Пети, который мог выиграть своим первым ходом.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит одна куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) убрать из кучи половину камней, если количество камней в куче делится на 2; иначе убрать из кучи два камня;
б) убрать из кучи две трети камней, если количество камней в куче делится на 3; иначе убрать из кучи три камня.
Например, пусть в куче 10 камней, тогда можно убрать половину или только три камня. А если в куче 12 камней, то можно убрать половину или две трети камней. Игра завершается в тот момент, когда в куче останется ровно 1 камень. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет ровно 1 камень. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 2. Определите, минимальное и максимальное значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит одна куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) убрать из кучи половину камней, если количество камней в куче делится на 2; иначе убрать из кучи два камня;
б) убрать из кучи две трети камней, если количество камней в куче делится на 3; иначе убрать из кучи три камня.
Например, пусть в куче 10 камней, тогда можно убрать половину или только три камня. А если в куче 12 камней, то можно убрать половину или две трети камней. Игра завершается в тот момент, когда в куче останется ровно 1 камень. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет ровно 1 камень. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 3. Найдите минимальное значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 20
Укажите наибольшее трёхзначное натуральное число, при вводе которого эта программа напечатает сначала 2, потом 7.
x = int(input())
a=0; b=1
while x > 0:
if x%2 > 0:
a += x%6
else:
b += x%6
x = x//6
print(a, b)
Вопрос 21
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1 2. Умножить на 2 3. Умножить на 3
Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 28 и при этом траектория вычислений содержит число 7?
Получите комплекты видеоуроков + онлайн версии
 0
0 944
944 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








