В предыдущей главе мы вывели зависимость плотности энергии излучения от частоты. Во многих задачах используются интегральные по спектру характеристики: плотность энергии, интенсивность и поток. Сначала вычислим плотность энергии. Затем определим понятия интенсивности и потока и выведем формулу для полной интенсивности. В конце главы сформулируем модель границы изотропного источника, в рамках которой справедлива формула Стефана-Больцмана.
3.1 Интегральная по спектру плотность энергииПроинтегрируем формулу (4.7) главы 2 по всему интервалу частот:
![]()
Переходя, как обычно, к безразмерной переменной
![]()
получим, что плотность энергии пропорциональна четвёртой степени температуры:
![]()
Вычислим безразмерный интеграл в правой части последней формулы. Он является частным случаем интегралов вида
![]()
соответствующим n = 4. Разложим дробь в подынтегральном выражении:
![]()
Искомый интеграл представляется в виде ряда
![]()
каждое слагаемое которого аналитически выражается через гамма-функцию
![]()
Следовательно,
![]()
Сумма в последней формуле известна как дзета–функция Римана:
![]()
Выпишем ряд её значений, некоторые из которых понадобятся нам в дальнейшем:
| n | (n) | |
|
| аналит. | число |
| 2 | π2/6 | 1.645 |
| 3 |
| 1.202 |
| 4 | π4/90 | 1.082 |
| 5 |
| 1.037 |
Функция (n) имеет аналитическое выражение при чётных значениях аргумента. Итак, множитель пропорциональности в формуле, выражающей зависимость плотности энергии U от температуры T:
(1.1) U = a·T4,
равен
![]()
В последней формуле присутствует постоянная Больцмана
k = 1.3802·10–16 эрг/К,
означающая, что температура в ней выражена в градусах Кельвина.
Иногда множитель a называют постоянной Стефана–Больцмана для плотности энергии. Используется также другая форма закона Стефана–Больцмана, связывающая полный поток F и температуру чёрного тела:
F = T4.
Чтобы определить величину , необходимо сформулировать модель, в которой поток от чёрного тела отличен от нуля. Такая модель будет изложена в следующих разделах, а сейчас вычислим полное число квантов Nф в единичном объёме чёрного тела. Для этого проинтегрируем по всем частотам формулу (4.8) второй главы:
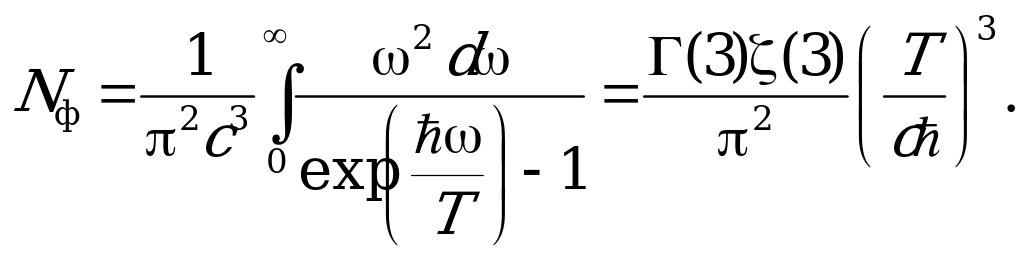
Если измерять температуру в градусах Кельвина, то
(1.3) Nф ≈ 20.3·T3.
В качестве примера оценим плотность числа фотонов реликтового излучения, температура которого, как известно, равна 2.73 К:
![]()
Последняя величина значительно превышает среднюю плотность частиц во Вселенной, которая по разным оценкам лежит в диапазоне от 10–3 см–3 до 10–6 см–3.
3.2 Основные понятия теории излученияОписание поля излучения основано на понятии интенсивности как энергии, протекающей через единичную площадку за единицу времени в заданном направлении в избранном интервале частот. Хотя интенсивность является характеристикой только поля излучения и не зависит от способа измерения, для её определения полезно ввести представление о некотором абстрактном приборе, который мы назовём «контрольной площадкой».
Контрольной площадкой будем считать плоскую поверхность небольших размеров (рис. 2.1), на которой задано направление. Обозначим через S её площадь, а n — перпендикулярный ей единичный вектор.
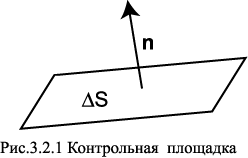
Направление излучения характеризуется двумя величинами: вектором k и телесным углом вокруг него. При известных k и говорят об «излучении в направлении k внутри телесного угла ». Иногда речь идёт просто об излучении в определённом направлении k, при этом телесный угол подразумевается.
ИнтенсивностьПонятие интенсивности даёт наиболее полное представление о пространственном и частотном распределении фотонов (при необходимости — и о состояниях поляризации).
Вначале сосредоточим внимание на той части излучения, которая проходит в направлении вектора n. Величины S и положим настолько малыми, что излучение можно считать однородным вдоль площадки и не зависящим от направления внутри телесного угла . Будем следить за прохождением излучения в течение столь короткого промежутка времени, что никакие его характеристики не успевают измениться. В таких условиях количество энергии E, протекшей через площадку за время t в интервале частот ω, пропорционально произведению S··ω·t. Следовательно, отношение
![]()
не зависит от размеров контрольной площадки, продолжительности измерения и выбранного угла раствора.
Но последнюю формулу ещё нельзя считать полноценной характеристикой поля излучения, так как осталась зависимость от направления площадки. Действительно, если наклонить площадку так, что векторы k и n образуют угол , то в том же самом поле излучения количество энергии, прошедшей через площадку, уменьшится пропорционально |cos|.
Величина энергии, протекающей сквозь площадку, пропорциональна площади её проекции на плоскость волнового фронта:
E S cos.
4

 Получите свидетельство
Получите свидетельство Вход
Вход











 Закон Стефана–Больцмана (62.5 KB)
Закон Стефана–Больцмана (62.5 KB)
 0
0 347
347 0
0 Нравится
0
Нравится
0


