Специально для учителей!

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Разработки / Математика / Практикумы / Прочее / Задачи СПУ.Раздаточный материал

Новогодняя распродажа готовых материалов для учителей! Скидки до 50 %

Задачи СПУ.Раздаточный материал

Раздаточный материал по теме "Решение задач СПУ" предназначен для выполнения алгоритма построения задач сетевого планирования и управления. В данной разработке предполагается решение задачи по всем пунктам. Каждый пункт решения содержит формулы и краткое пояснение для решения

Тетерина Светлана Владимировна

21.11.2017

Содержимое разработки

Условие задачи

Произвести комплекс работ по переводу магазина на самообслуживание. Исходные данные представлены в таблице 1. Составить сетевой график работ всего проекта; найти критический путь; найти ранние и поздние сроки свершения событий; определить резервы времени; сделать выводы.

Таблица 1

Работа	Содержание работы	Длительность (дни)
(1;2)	Составление сметы	15
(1;3)	Приобретение оборудования	16
(1;4)	Подбор кадров	6
(2;4)	Монтаж оборудования	6
(3;5)	Подготовка кадров	5
(4;6)	Оформление торгового зала	8
(5;6)	Доставка товаров	6
(5;7)	Заказ и получение форменной одежды	14
(5;8)	Заказ и получение ценников	8
(6;8)	Выкладка товаров	2
(7;8)	Заполнение ценников	4
(8;9)	Открытие магазина	3

Решение задачи

1.Построение сетевого графика (рис.1)

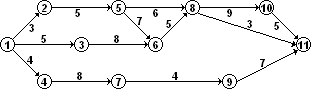
Рисунок 1

2.Нахождение критических путей

Т₁:125811=3+5+6+3=17 дня

Т₂:12581011=3+5+6+9+5=28 дней

Т₃:1256811==3+5+7+5+3=23 дня

Т₄:125681011==3+5+7+5+9+5=34 дня

Т₅:136811=5+8+5+3=21 дня

Т₆:13681011=5+8+5+9+5=31 дня

Т₇:147911=4+8+4+7=23 дня

Таким образом Т₄=Т_кр=34 дня

3.Находим ранние и поздние сроки свершения событий.

а) ранние сроки находятся согласно формулам (1)-(2)

t_p(9)= t_p(8)+ t_p(8;9)=39+3=42

а) поздние сроки находятся согласно формулам (3)-(4)

t_n_(з.с.)= t_p_(з.с.)= t_n(8)=42

t_n(8)= t_n(9)- t(8;9)=42-3=39

t_n(7)= t_n(8)- t(7;8)=39-4=35

t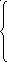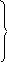_n(6)= t_n(8)- t(6;8)=39-2=37

t_n(6)- t(5;6)=37-6=31

=21

_n(5)=

t_n(7)- t(5;7)=35-14=21

t_n(8)- t(5;8)=39-8=31

t_n(4)= t_n(6)- t(4;6)=37-8=29

t_n(3)= t_n(5)- t(3;5)=21-5=16

t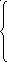_n(2)= t_n(4)- t(2;4)=29-6=23

t_n(2)- t(2;1)=23-15=8

t_n(1)= t_n(3)- t(3;1)=16-16=0

t_n(4)- t(4;1)=29-6=23

Полученные сроки свершения событий сводятся в таблицу 2

Таблица .2

Событие	1	2	3	4	5	6	7	8	9
t_p(i)	0	15	16	21	21	29	35	39	42
t_n(i)	0	23	16	29	21	37	35	39	42

Из таблицы видно, что события, принадлежащие критическому пути, имеют соответственно равные ранние и поздние сроки своего наступления.

4. Нахождение резервов времени выполнения работ и сведение в таблицу 3

Таблица 3

Работа (i,j)	t(i,j)	t_p(i)	t_n(i)	t_p(j)	t_n(j)	Резервы времени выполнения работ
Работа (i,j)	t(i,j)	t_p(i)	t_n(i)	t_p(j)	t_n(j)	ПР(i,j)	ГР(i,j)	СР(i,j)	НР(i,j)
(1;2)	15	0	0	15	23	8	8	0	0
(1;3)	16	0	0	16	16	0	0	0	0
(1;4)	6	0	0	21	29	23	23	15	15
(2;4)	6	15	23	21	29	8	0	0	-8
(3;5)	5	16	16	21	21	0	0	0	0
(4;6)	8	21	29	29	37	8	0	0	-8
(5;6)	6	21	21	29	37	10	0	2	2
(5;7)	14	21	21	35	35	0	0	0	0
(5;8)	8	21	21	39	39	10	10	10	10
(6;8)	2	29	37	39	39	8	0	8	0
(7;8)	4	35	35	39	39	0	0	0	0
(8;9)	3	39	39	42	42	0	0	0	0

Полный резерв рассчитывается из формулы (5), гарантийный резерв вычисляется согласно формуле (6), свободный резерв на основании формулы (7) и независимый резерв рассчитывается по формуле (8).

Из таблицы видно, что выполняются неравенства

НР(i,j)≤ ГР(i,j)≤ ПР(i,j) и НР(i,j)≤ СР(i,j)≤ ПР(i,j)

Выводы: Критический путь в рассматриваемой задаче один.

Т₄:135789

На нем нет резервов времени для выполнения работ.

Работы (1;4)=; (5;8) обладают всеми видами резервов времени

Полный и гарантийный резерв времени имеет работа (1;2).

Полный, свободный и независимый работа (5;6).

Полный и свободный работа (6;8).