Зачет по геометрии для 10 класса по теме "Векторы"

Билет № 1

1. Сформулируйте определение вектора, как изображается, обозначается вектор?

2. ВМ – медиана ∆АВС, О – произвольная точка пространства. Разложите вектор 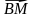по векторам , , .

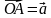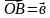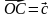Билет № 2

1. Длина вектора.

2. М – середина стороны АВ параллелограмма АВСД, О – произвольная точка пространства. Разложите вектор 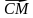по векторам , , .

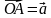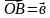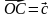Билет № 3

1. Сформулируйте определение нулевого вектора, единичного вектора.

2. О – точка пересечения диагоналей параллелограмма АВСД, М - произвольная точка пространства. Разложите вектор 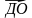по векторам , , .

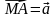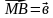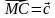Билет № 4

1. Какие векторы называются равными?

2. К – середина медианы АЕ ∆АВС, М – произвольная точка пространства. Разложите вектор 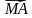по векторам , , .

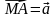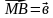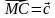Билет № 5

1. Сложение векторов: правило треугольника, параллелограмма, многоугольника, параллелепипеда.

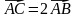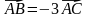2. Изобразите на рисунке взаимное расположение точек А, В и С, если: а) ; б) ; в) .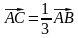

Билет № 6

1. Разность векторов.

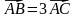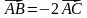2. Изобразите на рисунке взаимное расположение точек А, В и С, если: а) ; б) ; в) .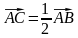

Билет № 7

1. Умножение вектора на число.

2. Точка С лежит на отрезке АВ и делит его в отношении 2:3, считая от вершины А. Выразите: а) вектор 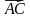через вектор 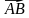; б) вектор 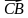через вектор 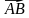; в) вектор через вектор .

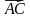Билет № 8

1. Свойства сложения векторов (с доказательством)

2. АВСДА₁В₁С₁Д₁ – параллелепипед. Упростите выражение 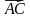+ ₁ + + + ₁ + .

Билет № 9

1. Свойства умножения вектора на число ( с доказательством)

2. АВСДА₁В₁С₁Д₁ – параллелепипед. Упростите выражение 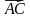₁ + + + ₁ + + _1.

Билет № 10

1. Какие векторы называются коллинеарными, сонаправленными, противоположно направленными, компланарными?

2. Точка А лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите: а) вектор через вектор 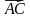; б) вектор 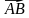через вектор ; в) вектор через вектор .

Билет № 11

1. Признак компланарности векторов.

2. АВСДА₁В₁С₁Д₁ – параллелепипед. Упростите выражение ₁ + ₁ + - ₁ + + .

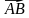Билет № 12

1. Разложение вектора по трем некомпланарным векторам.

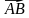2. АВСДА₁В₁С₁Д₁ – параллелепипед. Упростите выражение - + + ₁ + ₁ + ₁.

Билет № 13

1. Теорема о разложении вектора по трем некомпланарным векторам.

2.

Билет № 14

1. Сформулируйте определение вектора, как изображается, обозначается вектор?

2. Дан параллелепипед АВСДА₁В₁С₁Д_1. Медианы ∆ВВ₁С пересекаются в точке М. Разложите вектор по векторам ₁ = , = , = .

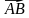Билет № 15

1. Длина вектора.

2.

Билет № 16

1. Сформулируйте определение нулевого вектора, единичного вектора.

2. Диагонали параллелепипеда АВСДА₁В₁С₁Д₁ пересекаются в точке О. При каком значении к справедливо соотношение 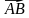+ ₁ + = к ?

Билет № 17

1. Какие векторы называются равными?

2. Диагонали параллелепипеда АВСДА₁В₁С₁Д₁ пересекаются в точке О. При каком значении к справедливо соотношение к( + + )= ?

Билет № 18

1. Сложение векторов: правило треугольника, параллелограмма, многоугольника, параллелепипеда.

2. Дан параллелепипед АВСДА₁В₁С₁Д₁. Медианы ∆А₁В₁С₁ пересекаются в точке К. Разложите вектор по векторам = , ₁ = , = .

Билет № 19

1. Разность векторов.

2. Дан параллелепипед АВСДА₁В₁С₁Д₁. Медианы ∆АД₁С пересекаются в точке М. Разложите вектор 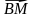по векторам = , ₁ = , = .

Билет № 20

1. Умножение вектора на число.

2. Изобразите тетраэдр АВСД и вектор, равный .

Билет № 21

1. Свойства умножения вектора на число ( с доказательством)

2. Изобразите тетраэдр АВСД и вектор, равный .

Билет № 22

1. Признак коллинеарности векторов.

2. Изобразите тетраэдр АВСД и вектор, равный .

Билет № 23

1. Какие векторы называются коллинеарными, сонаправленными, противоположно направленными, компланарными?

2. Изобразите тетраэдр АВСД и вектор, равный .

Билет № 24

1. Признак компланарности векторов.

2. Ребро куба АВСДА₁В₁С₁Д₁ равно 1. Найдите

Билет № 25

1. Разложение вектора по трем некомпланарным векторам.

2. ДАВС – правильная треугольная пирамида. Сторона основания равна . Боковые ребра наклонены к основанию под углом 60^о. Найдите .

Билет № 26

1. Теорема о разложении вектора по трем некомпланарным векторам.

2. АВСДА₁В₁С₁Д₁ – параллелепипед. Найдите ₁.