Зачет №2 по геометрии. Тема "Перпендикулярность прямых и плоскостей". 10 класс

Зачет №2 по теме «Перпендикулярность прямых и плоскостей»

Карточка№1

1. Через любую точку пространства проходит прямая, … к данной плоскости, и …

2. Двугранным углом называется фигура, образованная … и двумя полуплоскостями с общей границей а, …

3. Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?

4. Через сторону ВС треугольника АВС проведена плоскость α. АО – перпендикуляр к плоскости α. Назовите угол между АС и плоскостью α.

5. Верно ли, что если одна из двух плоскостей проходит через прямую, перпендикулярную к линии пересечения плоскостей, то эти плоскости перпендикулярны?

6. a α, Тогда прямые a и b не могут быть…

1) перпендикулярными;

2) параллельными;

3) скрещивающимися.

1. aǁb, ac. Прямые b и с не могут быть…

1) параллельными; 2) перпендикулярными; 3) скрещивающимися.

1. Даны прямые a и b и плоскость α. Определите угол между данными прямыми, если a α, b || α.

2. Не может плоскость быть не перпендикулярной данной плоскости, если она проходит через прямую…

1) параллельную данной плоскости;

2) перпендикулярную данной плоскости;

3) не перпендикулярную данной плоскости.

1. Какое утверждение верное?

1) Не может ребро двугранного угла быть не перпендикулярным любой прямой, лежащей в плоскости его линейного угла.

2) Не могут быть две плоскости, перпендикулярные третьей, непараллельными.

3) Не могут быть две плоскости, перпендикулярные одной плоскости, непараллельными.

1. AC = 16 см, BD = 6 см.

Тогда AD = …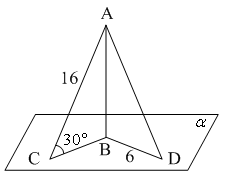

1. В прямоугольном параллелепипеде измерения равны 5, 7, 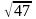. Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.

1. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости α, а катет наклонен к этой плоскости под углом 30°. Найдите угол между плоскостью α и плоскостью треугольника.

1. Из вершины А прямоугольного треугольника АВС (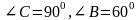 ) восстановлен перпендикуляр к плоскости АВС и на нем взят отрезок АМ = h. Точка М соединена с В и С. Найдите если двугранный угол АВСМ равен 30^°.

Зачет №2 по теме «Перпендикулярность прямых и плоскостей»

Карточка№2

1. Проекцией точки на плоскость называется основание …, проведенного из этой точки к плоскости, если точка …, и сама точка, если …

2. Прямая, проведенная в плоскости через основание … перпендикулярно к её … на эту плоскость, …..и к самой наклонной.

3. Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется ….

4. Даны прямые a, b, c и плоскость α. Укажите среди данных прямых прямую, перпендикулярную к двум другим, если a 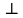α, b || α, с лежит в плоскости α.

5. Верно ли, что расстояние между параллельными плоскостями равно расстоянию от любой прямой одной плоскости до другой плоскости?

6. Д иагональ АС квадрата ABCD перпендикулярна некоторой плоскости 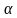, проходящей через точку А. Тогда диагональ BD…

1) перпендикулярна плоскости ;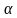

2) параллельна плоскости ;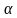

3) лежит в плоскости .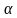

1. Какое утверждение неверное?

1) Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

2) Через точку, не лежащую на данной прямой, можно построить только одну плоскость, перпендикулярную данной прямой.

3) Через точку, не лежащую на данной прямой, можно построить только одну прямую, перпендикулярную данной прямой.

1. Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?

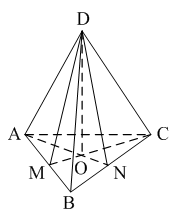2.  ABC, AN и CM – высоты. DO(ABC). Градусная мера угла ABCD равна градусной мере угла…

1) ABD;

2) AND;

3) ACD.

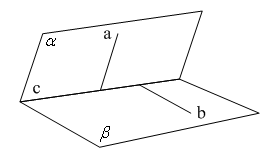
1. Тогда – это линейный угол двугранного угла между плоскостями и , если…

1 )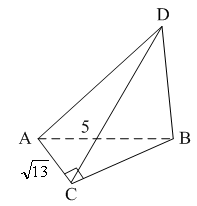

2)

3)

1. ABC, , АВ=5см, . BD(ABC), Тогда длина перпендикуляра BD равна…

1. В прямоугольном параллелепипеде измерения равны 6, 8, 10. Найти диагональ параллелепипеда и угол между диагональю параллелепипеда и плоскостью его основания.

1. Ребро CD тетраэдра ABCD перпендикулярно к плоскости АВС, АВ = ВС = АС = 6, BD = . Найдите двугранные углы DACB, DABC, BDCA.

1. Точка М находится на расстоянии h от плоскости . Проведены две наклонные МР и МQ (где Р и Q – основания наклонных), соответственно под углами 45^° и 60^°. Найдите РQ, если = 150^°, где О – основание перпендикуляра МО, МО